题目内容
(1)用“<”、“>”、“=”填空:
32+42______2×3×4;
22+(-7)2______2×2×(-7);
(-6)2+(-8)2______2×(-6)×(-8);
52+52______2×5×5.
(2)根据上式规律,用字母总结出结论为______.用所学知识试着说明一下.
解:(1)∵32+42=25,2×3×4=24,
∴32+42>2×3×4,
∵22+(-7)2=53,2×2×(-7)=-28,
∴22+(-7)2>2×2×(-7),
∵(-6)2+(-8)2=100,2×(-6)×(-8)=96,
∴(-6)2+(-8)2>2×(-6)×(-8),
∵52+52=50,2×5×5=50,
∴52+52=2×5×5,
故答案为:>,>,>,=.
(2)根据上式规律,用字母总结出结论为a2+b2≥2ab,
理由是:∵(a-b)2≥0,
∴a2+b2-2ab≥0,
∴a2+b2≥2ab,
故答案为:a2+b2≥2ab.
分析:(1)求出每个式子的值,再判断大小即可.
(2)根据(1)的结果和算式规律得出即可.
点评:本题考查了完全平方公式的应用,主要考查学生的理解能力和计算能力.
∴32+42>2×3×4,
∵22+(-7)2=53,2×2×(-7)=-28,
∴22+(-7)2>2×2×(-7),
∵(-6)2+(-8)2=100,2×(-6)×(-8)=96,
∴(-6)2+(-8)2>2×(-6)×(-8),
∵52+52=50,2×5×5=50,
∴52+52=2×5×5,
故答案为:>,>,>,=.
(2)根据上式规律,用字母总结出结论为a2+b2≥2ab,
理由是:∵(a-b)2≥0,
∴a2+b2-2ab≥0,
∴a2+b2≥2ab,
故答案为:a2+b2≥2ab.
分析:(1)求出每个式子的值,再判断大小即可.
(2)根据(1)的结果和算式规律得出即可.
点评:本题考查了完全平方公式的应用,主要考查学生的理解能力和计算能力.

练习册系列答案
相关题目

 答下列问题:
答下列问题: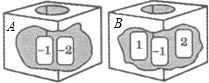 的卡片,它们分别写有数字1,-1,2.现从A箱、B箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
的卡片,它们分别写有数字1,-1,2.现从A箱、B箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求: