题目内容
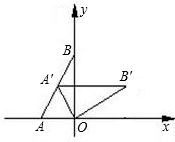 如图,点A在x轴的负半轴上,点B在y轴的正半轴上,∠ABO=30°,AO=2,将△AOB绕原点O顺时针旋转后得到△A′OB′.当点A′恰好落在AB上时,点B′的坐标为
如图,点A在x轴的负半轴上,点B在y轴的正半轴上,∠ABO=30°,AO=2,将△AOB绕原点O顺时针旋转后得到△A′OB′.当点A′恰好落在AB上时,点B′的坐标为分析:如图,由于将△AOB绕原点O顺时针旋转后得到△A'OB′.当点A′恰好落在AB上时,根据旋转的旋转知道A'O=AO,而∠ABO=30°,由此得到∠A=60°,所以是将△AOB绕原点O顺时针旋转60°后得到△A'OB′,由此可以求∠B'OC=30°,而AO=2,可以求出OB′=OB=2
,过B′作B′C⊥OC于C,解直角三角形B′OC即可求出点B′的坐标.
| 3 |
解答: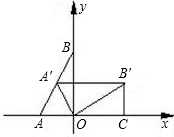 解:如图,∵将△AOB绕原点O顺时针旋转后得到△A'OB′,
解:如图,∵将△AOB绕原点O顺时针旋转后得到△A'OB′,
当点A′恰好落在AB上时,
∴A'O=AO,
而∠ABO=30°,
∴∠A=60°,
∴△A'OA是等边三角形,
∴是将△AOB绕原点O顺时针旋转60°后得到△A'OB′,
∴∠B'OC=30°,
而AO=2,
∴OB′=OB=2
,
过B′作B′C⊥OC于C,
∴B′C=
,OC=3,
∴点B′的坐标为(3,
).
故填空答案:(3,
).
 解:如图,∵将△AOB绕原点O顺时针旋转后得到△A'OB′,
解:如图,∵将△AOB绕原点O顺时针旋转后得到△A'OB′,当点A′恰好落在AB上时,
∴A'O=AO,
而∠ABO=30°,
∴∠A=60°,
∴△A'OA是等边三角形,
∴是将△AOB绕原点O顺时针旋转60°后得到△A'OB′,
∴∠B'OC=30°,
而AO=2,
∴OB′=OB=2
| 3 |
过B′作B′C⊥OC于C,
∴B′C=
| 3 |
∴点B′的坐标为(3,
| 3 |
故填空答案:(3,
| 3 |
点评:解决本题的关键是正确理解题目,按题目的叙述一定要把各点的大致位置确定,正确地作出图形.

练习册系列答案
相关题目
 转90°,得到△A1B1O,再继续旋转90°,得到△A2B2O.抛物线y=ax2+bx+3经过B、B1两点.
转90°,得到△A1B1O,再继续旋转90°,得到△A2B2O.抛物线y=ax2+bx+3经过B、B1两点. 如图,点A在x轴的负半轴上,OA=4,AB=OB=
如图,点A在x轴的负半轴上,OA=4,AB=OB= 已知:如图,点B在y轴的负半轴上,点A在x轴的正半轴上,且OA=2,tan∠OAB=2.
已知:如图,点B在y轴的负半轴上,点A在x轴的正半轴上,且OA=2,tan∠OAB=2.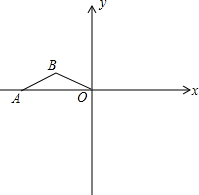 如图,点A在x轴的负半轴上,OA=4,AB=OB=
如图,点A在x轴的负半轴上,OA=4,AB=OB= ,将△ABO绕坐标原点O顺时针旋转90°,得到△A1B1O,再继续旋转90°,得到△A2B2O,抛物线y=ax2+bx+3经过B、B1两点.
,将△ABO绕坐标原点O顺时针旋转90°,得到△A1B1O,再继续旋转90°,得到△A2B2O,抛物线y=ax2+bx+3经过B、B1两点.