Question

【题目】如图，边长为4的正方形ABCD内接于⊙O，E是弧AB上的一动点(不与A，B重合)，F是弧BC上的一点，连接OE，OF，分别与AB，BC交于点G，H，且∠EOF＝90°，有以下结论：①＝；②△OGH是等腰直角三角形；③四边形OGBH的面积随着点E位置的变化而变化；④△OGH周长的最小值为4＋.其中正确的是(　　)

A. ①③④ B. ①②③ C. ①② D. ③④

Answer 1

【答案】C

【解析】①连接OA，OB，根据正方形的性质，知∠AOB=90°=∠EOF，又∠BOE共用，故可得∠AOE=∠BOF，再根据圆心角定理可得①＝；故①正确；

②连接OB，OC，证明△OGB≌△OHC，可得OG=OH，即可得出△OGH是等腰直角三角形；故②正确；

③过点O作OM⊥BC，ON⊥AB，易证得△OGN≌△OHM，因此可得出S△OGN=S△OHM，故不管点E的位置如何变化，四边形OGBH的面积不变；故③错误；

④过点B作B关于OF的对称点P（易知点P在⊙O上），连接PH，则PH=BH；过点B作B关于OE的对称点Q（易知点Q在⊙O上），连接QG，则QG=BG；连接PQ，易证明PQ过圆心O，则PQ==4≠４＋，故④错误.

①如图所示，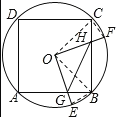

∵∠BOE+∠BOF=90°，∠COF+∠BOF=90°，
∴∠BOE=∠COF，
在△BOE与△COF中，

∴△BOE≌△COF，
∴BE=CF，
∴ ，①正确；
②∵BE=CF，
∴△BOG≌△COH；
∵∠BOG=∠COH，∠COH+∠OBF=90°，
∴∠GOH=90°，OG=OH，
∴△OGH是等腰直角三角形，②正确．
③如图所示，

∵△HOM≌△GON，
∴四边形OGBH的面积始终等于正方形ONBM的面积，③错误；
④过点B作B关于OF的对称点P（易知点P在⊙O上），连接PH，则PH=BH；过点B作B关于OE的对称点Q（易知点Q在⊙O上），连接QG，则QG=BG；

连接PQ，易证明PQ过圆心O，

∴PQ==4≠４＋，

故④错误.

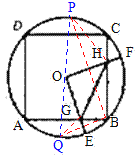
综上，①②正确，③④错误.

故选：C