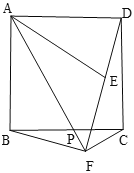
题目内容
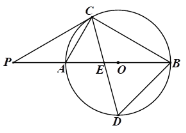
【题目】如图,已知![]() 为
为![]() 的直径,
的直径,![]() 、
、![]() 是
是![]() 的弦,
的弦,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,
,![]() ,
,![]() 、
、![]() 的延长线相交于点
的延长线相交于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
(3)在(2)中的条件下,![]() ,将
,将![]() 以点
以点![]() 为中心逆时针旋转
为中心逆时针旋转![]() ,求
,求![]() 扫过的图形的面积(结果用
扫过的图形的面积(结果用![]() 表示).
表示).
【答案】(1)见解析;(2)圆![]() 的半径为4;(3)BD扫过的图形的面积为
的半径为4;(3)BD扫过的图形的面积为![]()
【解析】
(1)如图1(见解析),连接DO,先根据平行线的性质和等腰三角形的性质推出![]() ,再由
,再由![]() 定理判定
定理判定![]() ,从而可得
,从而可得![]() ,最后根据圆的切线的判定定理即可证;
,最后根据圆的切线的判定定理即可证;
(2)根据题(1)的结论,在![]() 中,利用勾股定理即可得;
中,利用勾股定理即可得;
(3)如图2(见解析),先确定阴影部分为BD所扫过的图形,再利用扇形和三角形的面积公式求解即可.
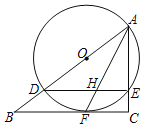
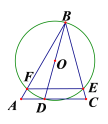
(1)如图1,连结![]()
∵![]()
∴![]()
又∵![]()
∴![]()
∴![]()
在![]() 和
和![]() 中,
中,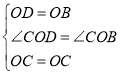
![]()
∴![]()
∵![]() 是圆
是圆![]() 的切线
的切线
∴![]()
∴![]()
又∵点![]() 在圆
在圆![]() 上,OD为圆O的半径
上,OD为圆O的半径
∴![]() 是圆
是圆![]() 的切线;
的切线;
(2)如图1,设圆![]() 的半径为r
的半径为r
则![]()
由题(1)的结论,![]() 是直角三角形
是直角三角形
则![]() ,即
,即![]() ,解得
,解得![]()
故圆![]() 的半径为4;
的半径为4;
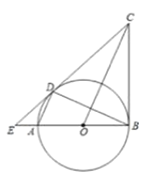
(3)如图2,由旋转的过程得:阴影部分为BD所扫过的图形
由题(2)可知![]()
![]()
![]()
![]()
![]()
由旋转的性质得,![]() 和
和![]() 的面积相等
的面积相等
则![]() 所扫过的图形面积为:
所扫过的图形面积为:![]()
空白区域的面积为:![]()
因此,![]()
故![]() 扫过的图形的面积为
扫过的图形的面积为![]() .
.


练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目