题目内容
 如图,E、F、G、H分别是正方形ABCD各边的中点,要使中间阴影部分小正方形的面积是25,那么大正方形的边长应该是
如图,E、F、G、H分别是正方形ABCD各边的中点,要使中间阴影部分小正方形的面积是25,那么大正方形的边长应该是
- A.10
- B.5

- C.7.5
- D.5

B
分析:首先设GP=x,GC=y;表示出阴影部分的边长,易得△CGP∽△CHD,根据相似三角形的性质,易得x与y之间的关系,解可得y的值;进而可得大正方形边长.
解答: 解:设阴影部分正方形的顶点为MNPQ(如下图所示),设GP=X,则BN=2X,设GC=Y,则BC=2Y
解:设阴影部分正方形的顶点为MNPQ(如下图所示),设GP=X,则BN=2X,设GC=Y,则BC=2Y
显然△CGP∽△CHD,则 ?x=
?x=
由勾股定理得,Y2+(2Y)2=(X+2X+5)2
联合以上两式解得,Y= ,即大正方形边长为
,即大正方形边长为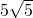
故选B.
点评:本题涉及正方形、相似三角形的相关性质和勾股定理,难度中上.
分析:首先设GP=x,GC=y;表示出阴影部分的边长,易得△CGP∽△CHD,根据相似三角形的性质,易得x与y之间的关系,解可得y的值;进而可得大正方形边长.
解答:
 解:设阴影部分正方形的顶点为MNPQ(如下图所示),设GP=X,则BN=2X,设GC=Y,则BC=2Y
解:设阴影部分正方形的顶点为MNPQ(如下图所示),设GP=X,则BN=2X,设GC=Y,则BC=2Y显然△CGP∽△CHD,则
 ?x=
?x=
由勾股定理得,Y2+(2Y)2=(X+2X+5)2
联合以上两式解得,Y=
 ,即大正方形边长为
,即大正方形边长为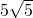
故选B.
点评:本题涉及正方形、相似三角形的相关性质和勾股定理,难度中上.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.