题目内容
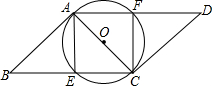 如图,平行四边形ABCD中,E、F分别是BC、AD边上的点,四边形AECF是⊙O的内接四边形,且AC是⊙O的直径.
如图,平行四边形ABCD中,E、F分别是BC、AD边上的点,四边形AECF是⊙O的内接四边形,且AC是⊙O的直径.(1)求证:BE=DF;
(2)若BA与⊙O相切,BC=10cm,BE:CE=3:2,求AC的长.
考点:切线的性质,全等三角形的判定与性质,平行四边形的性质
专题:证明题
分析:(1)根据平行四边形的性质得到AB=CD,∠B=∠D,再根据圆周角定理得到∠AEB=∠CFD=90°,则可利用“AAS”判断△ABE≌△CDF,所以BE=DF;
(2)根据切线的性质得∠BAC=90°,由于BC=10cm,BE:CE=3:2,则CE=4cm,再证明Rt△CAE∽Rt△CBA,所以CA:CB=CE:CA,即CA:10=4:CA,然后解方程得到AC的长.
(2)根据切线的性质得∠BAC=90°,由于BC=10cm,BE:CE=3:2,则CE=4cm,再证明Rt△CAE∽Rt△CBA,所以CA:CB=CE:CA,即CA:10=4:CA,然后解方程得到AC的长.
解答:(1)证明:∵四边形ABCD为平行四边形,
∴AB=CD,∠B=∠D,
∵AC是⊙O的直径,
∴∠AEC=∠AFC=90°,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中
,
∴△ABE≌△CDF,
∴BE=DF;
(2)解:∵BA与⊙O相切,
∴∠BAC=90°,
∵BC=10cm,BE:CE=3:2,
∴CE=4cm,
∵∠ACE=∠BCA,
∴Rt△CAE∽Rt△CBA,
∴CA:CB=CE:CA,即CA:10=4:CA,
∴CA=2
(cm).
∴AB=CD,∠B=∠D,
∵AC是⊙O的直径,
∴∠AEC=∠AFC=90°,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中
|
∴△ABE≌△CDF,
∴BE=DF;
(2)解:∵BA与⊙O相切,

∴∠BAC=90°,
∵BC=10cm,BE:CE=3:2,
∴CE=4cm,
∵∠ACE=∠BCA,
∴Rt△CAE∽Rt△CBA,
∴CA:CB=CE:CA,即CA:10=4:CA,
∴CA=2
| 10 |
点评:本题考查了切线的性质:圆的切线垂直于过切点的半径.也考查了圆周角定理、平行四边形的性质以及三角形全等、相似的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列运算中,计算正确的是( )
| A、2a2+3a3=5a5 |
| B、2a2+3a2=5a4 |
| C、2a2•3a2=6a4 |
| D、2a2•3a3=5a6 |

 如图,已知在菱形ABCD中,DE⊥AB,DF⊥BC,垂足分别为E、F,且AE=BE,则∠EDF=
如图,已知在菱形ABCD中,DE⊥AB,DF⊥BC,垂足分别为E、F,且AE=BE,则∠EDF= 如图,已知BF=CE,∠A=∠D,∠B=∠E,则AC=DF吗?请说明理由.
如图,已知BF=CE,∠A=∠D,∠B=∠E,则AC=DF吗?请说明理由. 如图,已知A,B两点的坐标分别为(-3,0),(0,3),⊙C的圆心坐标为(3,0),并与x轴交于坐标原点O.若E是⊙C上的一个动点,线段AE与y轴交于点D.
如图,已知A,B两点的坐标分别为(-3,0),(0,3),⊙C的圆心坐标为(3,0),并与x轴交于坐标原点O.若E是⊙C上的一个动点,线段AE与y轴交于点D.