题目内容
 如图,DE是△ABC的中位线,F,G分别是BD,CE中点,如果DE=6,那么FG的长是________.
如图,DE是△ABC的中位线,F,G分别是BD,CE中点,如果DE=6,那么FG的长是________.
9
分析:首先利用三角形的中位线的性质求得BC的长,得到四边形DBCE是梯形;又由梯形中位线的性质求得FG的长.
解答:∵DE是△ABC的中位线,DE=6,
∴DE∥BC,DE= BC,
BC,
∴BC=2DE=12,
∵F,G分别是BD,CE中点,
∴FG= (DE+BC)=
(DE+BC)= ×(6+12)=9.
×(6+12)=9.
故答案为:9.
点评:此题考查了梯形中位线与三角形中位线的性质.题目难度不大,注意数形结合思想的应用.
分析:首先利用三角形的中位线的性质求得BC的长,得到四边形DBCE是梯形;又由梯形中位线的性质求得FG的长.
解答:∵DE是△ABC的中位线,DE=6,
∴DE∥BC,DE=
 BC,
BC,∴BC=2DE=12,
∵F,G分别是BD,CE中点,
∴FG=
 (DE+BC)=
(DE+BC)= ×(6+12)=9.
×(6+12)=9.故答案为:9.
点评:此题考查了梯形中位线与三角形中位线的性质.题目难度不大,注意数形结合思想的应用.

练习册系列答案
相关题目
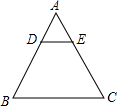 已知:如图,DE是△ABC的中位线,若AD=4,AE=5,BC=12,则△ADE的周长为( )
已知:如图,DE是△ABC的中位线,若AD=4,AE=5,BC=12,则△ADE的周长为( )| A、7.5 | B、15 | C、30 | D、24 |
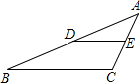 如图,DE是△ABC的中位线,则△ADE和四边形BCED的面积之比为( )
如图,DE是△ABC的中位线,则△ADE和四边形BCED的面积之比为( )| A、1:2 | B、1:3 | C、1:4 | D、以上都不对 |
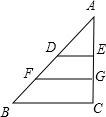 如图,DE是△ABC的中位线,FG是梯形BCED的中位线,若BC=16cm,则FG的长是( )
如图,DE是△ABC的中位线,FG是梯形BCED的中位线,若BC=16cm,则FG的长是( )| A、6 | B、8 | C、10 | D、12 |
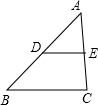 如图,DE是△ABC的中位线,若BC=6,则DE=
如图,DE是△ABC的中位线,若BC=6,则DE= 16、已知:如图,DE是△ABC的中位线,点P是DE的中点,CP的延长线交AB于点Q,那么S△DPQ:S△ABC=
16、已知:如图,DE是△ABC的中位线,点P是DE的中点,CP的延长线交AB于点Q,那么S△DPQ:S△ABC=