Question

【题目】如图，已知菱形OABC的边OA在x轴上，点B的坐标为(8，4)，P是对角线OB上的一个动点，点D(0，1)在y轴上，当PC＋PD最短时，点P的坐标为________．

Answer 1

【答案】（，）

【解析】

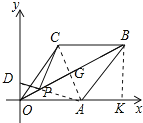
如图连接AC，AD，分别交OB于G、P，作BK⊥OA于K．首先说明点P就是所求的点，再求出点B坐标，求出直线OB、DA，列方程组即可解决问题．

解：如图连接AC，AD，分别交OB于G、P，作BK⊥OA于K．

在Rt△OBK中，OB===4，

∵四边形OABC是菱形，

∴AC⊥OB，GC=AG，OG=BG=2，

设OA=AB=x，

在Rt△ABK中，

∵AB2=AK2+BK2，

∴x2=（8-x）2+42，

∴x=5，

∴A（5，0），

∵A、C关于直线OB对称，

∴PC+PD=PA+PD=DA，

∴此时PC+PD最短，

∵直线OB解析式为y=x，直线AD解析式为y=-x+2，

由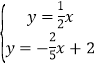

解得，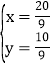

∴点P坐标（，），

故答案为（，）.