题目内容
已知抛物线y=x2-2bx+c(c>0)与y轴的交点为A,顶点为M(m,n).
(1)若c=2b-1,点M在x轴上,求c的值.
(2)若直线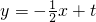 过点A,且与x轴交点为B,直线和抛物线的另一交点为P,且P为线段AB的中点.当n取得最大值时,求抛物线的解析式.
过点A,且与x轴交点为B,直线和抛物线的另一交点为P,且P为线段AB的中点.当n取得最大值时,求抛物线的解析式.
 解:(1)把c=2b-1代入y=x2-2bx+c得:y=x2-2bx+2b-1,
解:(1)把c=2b-1代入y=x2-2bx+c得:y=x2-2bx+2b-1,∴M(m,n)的坐标为
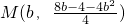 ,
,∵M在x轴上,
∴
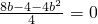 ,即b2-2b+1=0,
,即b2-2b+1=0,解得:b=1,
∴c=2b-1=1.
(2)过P作PD⊥x轴,
∵A(0,c),
∴
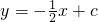 ,
,∴B(2c,0),
∴
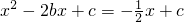 ,即
,即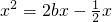 ,
,解得:
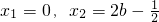 ,
,∵PD∥AD,
∴
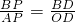 ,
,∵P为AB中点,
∴
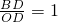 ,
,∴OD=c,
∴
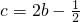 ,
,∴抛物线的解析式为:y=x2-2bx+2b-
 ,
,∴
 =
=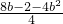 =
=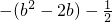 =
=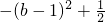 ,
,∵-1<0,
∴二次函数开口向下,存在最大值,
∴当b=1时,n的最大值为
 ,
,∴
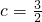 ,
,∴
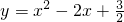 .
.分析:(1)将c的值代入抛物线,确定抛物线的顶点坐标,再由点M在x轴上,可得关于b的方程,解出可得出b的值,继而得出c的值;
(2)过P作PD⊥x轴,根据直线解析式确定点B的坐标,联立抛物线与直线解析式求出交点坐标,由P为AB中点,可得
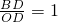 ,从而得出c的值,用含b的式子表示出抛物线解析式,表示出n的值,利用配方法求最值即可.
,从而得出c的值,用含b的式子表示出抛物线解析式,表示出n的值,利用配方法求最值即可.点评:本题考查了二次函数的综合,涉及了二次函数的顶点坐标公式、配方法求二次函数最值,解答本题关键是熟练运用等量代换的运用,难度较大,同学们注意培养自己解答综合题的能力.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.