题目内容

如图，在矩形OABC中，点B的坐标为（-2，3）．
（1）画出矩形OABC绕点O顺时针旋转90°后的矩形OA1B1C1，并直接写出点A1、B1、C1的坐标．
（2）求出线段OB在旋转过程中所扫过的部分面积．
分析：（1）根据旋转中心为点O，旋转角度为90度，旋转方向为顺时针可找到各点的对应点，顺次连接即可得出旋转后的图形．
（2）计算出扫过的面积即是扇形OBB'的面积，根据扇形的面积公式运算即可得出答案．
解答：解：（1）根据旋转中心为点O，旋转角度为90度，旋转方向为顺时针可找到各点的对应点，顺次连接，所作图形如下：

结合坐标图可得：A1（0，2），B1（3，2），C1（3，0）．
（2）线段OB=
(-2)2+32
=
13
，线段OB扫过的面积为扇形OBB'的面积，
∴S扇形OBB'=
nπR2
360
=
90π(
13
)2
360
=
13π
4
．
点评：此题考查了旋转作图及扇形的面积计算，解答本题的关键是仔细审题得到旋转的三要素：①旋转中心、②旋转角度、③旋转方向，另外要熟练扇形的面积公式．
练习册系列答案
相关题目
如图，在矩形OABC中，已知A、C两点的坐标分别为A（4，0）、C（0，2），D为OA的中点．设点这P是∠AOC平分线上的一个动点（不与点O重合）．
（1）填空：无论点P运动到何处，PC
 
PD（填“＞”、“＜”或“=”）；
（2）当点P运动到与点B的距离最小时，试确定过O、P、D三点的抛物线的解析式；
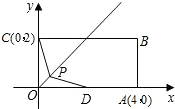（3）设点E是（2）中所确定抛物线的顶点，当点P运动到何处时，△PDE的周长最小？求精英家教网出此时点P的坐标和△PDE的周长．
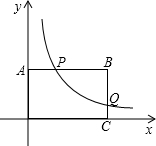如图，在矩形OABC中，已知A、C两点的坐标分别为A（4，0）、C（0，2），D为OA的中点．设点P是∠AOC精英家教网平分线上的一个动点（不与点O重合）．
（1）试证明：无论点P运动到何处，PC总与PD相等；
（2）当点P运动到与点B的距离最小时，试确定过O、P、D三点的抛物线的解析式；
（3）设点E是（2）中所确定抛物线的顶点，当点P运动到何处时，△PDE的周长最小？求出此时点P的坐标和△PDE的周长；
（4）设点N是矩形OABC的对称中心，是否存在点P，使∠CPN=90°？若存在，请直接写出点P的坐标．
如图，在矩形OABC中，AB∥x轴．函数y=
1x
(x＞0)的图象分别交AB、BC边于P、Q两点，且P是精英家教网AB的中点，设点P的横坐标为a．
（1）用含a的代数式表示点Q的坐标．
（2）试说明点Q是BC的中点．
（2012•莆田质检）如图，在矩形OABC中，OA、OC两边分别在x轴、y轴的正半轴上，OA=3，OC=2，过OA边上的D点，沿着BD翻折△ABD，点A恰好落在BC边上的点E处，反比例函数y=
kx
（k＞0）在第一象限上的图象经过点E与BD相交于点F．
（1）求证：四边形ABED是正方形；
（2）点F是否为正方形ABED的中心？请说明理由．
（2013•永春县质检）如图，在矩形OABC中，点A、C的坐标分别是（a，0），（0，
3
），点D是线段BC上的动点（与B、C不重合），过点D作直线l：y=-
3
x+b交线段OA于点E．
（1）直接写出矩形OABC的面积（用含a的代数式表示）；
（2）已知a=3，当直线l将矩形OABC分成周长相等的两部分时
①求b的值；
②梯形ABDE的内部有一点P，当⊙P与AB、AE、ED都相切时，求⊙P的半径．
（3）已知a=5，若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1，设CD=k，当k满足什么条件时，使矩形OABC和四边形O1A1B1C1的重叠部分的面积为定值，并求出该定值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网