题目内容
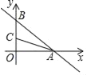
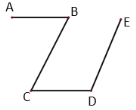
【题目】(1)如图,![]() 求证
求证![]()
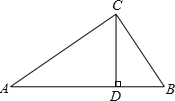
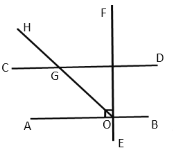
(2)如图,![]() 为垂足,
为垂足,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .求
.求![]() 的度数.
的度数.
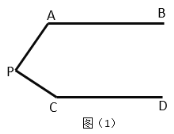
(3)已知![]()
①如图1,求![]() 的度数;
的度数;
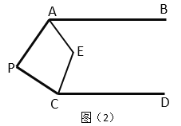
②如图2,![]() 和
和![]() 的平分线
的平分线![]() 相交于点
相交于点![]() ,求
,求![]() 的度数;
的度数;
③在图2中,画![]() 和
和![]() 平分线相交于点
平分线相交于点![]() ,求
,求![]() 的度数(直接写出结果即可)
的度数(直接写出结果即可)
【答案】(1)见解析;(2) ![]() ;(3) ①
;(3) ①![]() ;②
;②![]() ;③画图见解析,
;③画图见解析,![]() .
.
【解析】
(1)先观察题目中的图形,结合题目的信息找到判定直线平行的条件,运用同旁内角互补两直线平行即可证明;
(2)运用平行的性质,两直线平行,内错角相等,再通过计算即可得到答案;
(3) ①连接AC,运用直线平行的性质和三角形的内角和等于180°即可得到答案;
②连接AC,运用直线平行的性质和角平分线的性质以及四边平的内角和等于360°即可得到答案;
③先作图,再和②一样计算即可得到答案;
(1)证明:![]() ,
,
∴∠B=∠C(两直线平行,内错角相等),
又∵![]() ,
,
∴![]() (等量替换),
(等量替换),
∴![]() (同旁内角互补,两直线平行).
(同旁内角互补,两直线平行).
(2)证明:![]() ,
,
∴![]() (两直线平行,内错角相等),
(两直线平行,内错角相等),
又∵![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3) ①如图,连接AC,

∵![]() ,
,
∴![]() (两直线平行,同旁内角互补),
(两直线平行,同旁内角互补),
又∵![]() ,
,
∴![]()
∴![]() ;
;
②由①知![]() ,
,
又∵![]() 和
和![]() 的平分线
的平分线![]() 相交于点
相交于点![]() ,
,
∴![]() ,
,
∴![]() ;
;
③画图如下:

直接写出∠F的度数为:![]() ;
;

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目