题目内容
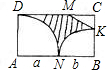 如图,在长方形ABCD中,DM:MC=2:1,AN=a,NB=b,DN是以A为圆心,a为半径的一段圆弧,NK是以B为圆心,b为半径的一段圆弧,则阴影部分的面积S阴=________.
如图,在长方形ABCD中,DM:MC=2:1,AN=a,NB=b,DN是以A为圆心,a为半径的一段圆弧,NK是以B为圆心,b为半径的一段圆弧,则阴影部分的面积S阴=________.
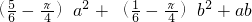
分析:阴影部分的面积=边长为a+b,a的长方形的面积-半径为a的
 圆的面积-半径为b的
圆的面积-半径为b的 圆的面积-直角边长为a-b,
圆的面积-直角边长为a-b, (a+b)的三角形的面积,把相关数值代入即可求解.
(a+b)的三角形的面积,把相关数值代入即可求解.解答:由题意得,CD=AB=a+b,AD=BC=a,NB=BK=b,
∴CK=a-b,
∵DM:MC=2:1,
∴MC=
 (a+b),
(a+b),∴阴影部分的面积=(a+b)a-
 ×π×a2-
×π×a2- ×π×b2-
×π×b2- ×(a-b)×
×(a-b)× (a+b),
(a+b),=a2+ab-
 -
- -
- (a2-b2),
(a2-b2),=
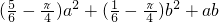 ,
,故答案为:
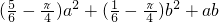 .
.点评:本题考查列代数式及化简,得到阴影部分的面积的等量关系解决本题的关键,易错点是得到各个图形相应的边长或半径.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
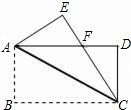 于点F.
于点F. 如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.
如图,在Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,以D作DE⊥AC与CB的延长线交于E,以AB、BE为邻边作长方形ABEF,连接DF,求DF的长.

