题目内容
已知直线l1经过点(3,5)与(-4,-9),直线l3∥l1,且过直线l2与y轴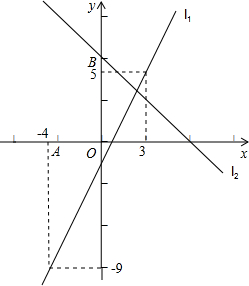 的交点B,交x轴于点A,已知直线l2:y=-x+6.
的交点B,交x轴于点A,已知直线l2:y=-x+6.(1)画出直线l3的位置,求出直线l1、l3的解析式和点A的坐标.
(2)若点P(x,y)是线段AB上的一动点,△OPA的面积为S,求:
①S关于x的函数关系式,并写出自变量x的取值范围;
②请求出S的最大值或最小值.
分析:(1)根据题意,用代入法求出直线l1、l3的解析式的表达式.因为l3交x轴于点A,根据坐标系的特征,求出A的坐标.
(2)①因为OA=3,P(x,y)是线段AB上的一动点,所以yp=2x+6>0,自变量x的取值范围是-3≤x≤0.根据三角形面积公式确定S关于x的函数关系式.
②根据一次函数的性质与自变量x的取值范围,确定最大值和最小值.
(2)①因为OA=3,P(x,y)是线段AB上的一动点,所以yp=2x+6>0,自变量x的取值范围是-3≤x≤0.根据三角形面积公式确定S关于x的函数关系式.
②根据一次函数的性质与自变量x的取值范围,确定最大值和最小值.
解答: 解:(1)直线l1经过点(3,5)与(-4,-9),设直线l1:y=k1x+b1.
解:(1)直线l1经过点(3,5)与(-4,-9),设直线l1:y=k1x+b1.
由
得
,
∴直线l1:y=2x-1.(1分)
当x=0时,y=-x+6=6,
∴B(0,6).
∵直线l3∥l1,
∴设直线l3y=2x+b3;
且l3过直线l2与y轴的交点B(0,6),
∴直线l3:y=2x+6,如图.
由2x+6=0得x=-3,
∴A(-3,0);
(2)①由A(-3,0)知OA=3.
∵点P(x,y)是线段AB上的一动点,
∴yp=2x+6>0,自变量x的取值范围是-3≤x≤0.
∴S=
OA•yp=
×3(2x+6)=3x+9,
∴S关于x的函数关系式是S=3x+9;
②由S=3x+9知3>0,∴y随x的增大而增大
又-3≤x≤0,
∴x=0时,S有最大值9.
当x=-3时,S有最小值时0.
 解:(1)直线l1经过点(3,5)与(-4,-9),设直线l1:y=k1x+b1.
解:(1)直线l1经过点(3,5)与(-4,-9),设直线l1:y=k1x+b1.由
|
|
∴直线l1:y=2x-1.(1分)
当x=0时,y=-x+6=6,
∴B(0,6).
∵直线l3∥l1,
∴设直线l3y=2x+b3;
且l3过直线l2与y轴的交点B(0,6),
∴直线l3:y=2x+6,如图.
由2x+6=0得x=-3,
∴A(-3,0);
(2)①由A(-3,0)知OA=3.
∵点P(x,y)是线段AB上的一动点,
∴yp=2x+6>0,自变量x的取值范围是-3≤x≤0.
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
∴S关于x的函数关系式是S=3x+9;
②由S=3x+9知3>0,∴y随x的增大而增大
又-3≤x≤0,
∴x=0时,S有最大值9.
当x=-3时,S有最小值时0.
点评:本题主要考查用代入法求出直线的解析式和根据一次函数的性质与自变量x的取值范围,确定最大值和最小值.

练习册系列答案
相关题目
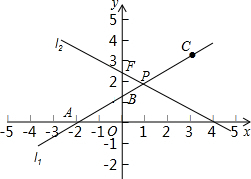 是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.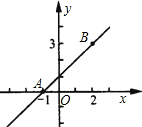 P(m,0).
P(m,0).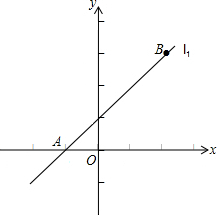 如图,已知直线l1经过点A(-1,0)和点B(2,3).
如图,已知直线l1经过点A(-1,0)和点B(2,3).