题目内容
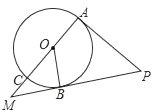
【题目】如图，
是正方形
的边
上一点，下列条件中：①
；②
；③
；④
；⑤
．其中能使
的有（ ）
A. ①②B. ①②③
C. ①②③④D. ①②③④⑤
【答案】D
【解析】
对于①②④，直接利用相似三角形的判定方法判断即可；对于③，先利用同角的余角相等转化为①，即可进行判断，对于⑤，利用比例的性质和勾股定理进行判断.
解：∵∠B=∠C=90°，∴只要满足
或
，均可判定△ABE∽△ECF，所以①②都正确；
③中，当
时，∵∠AEB+∠BAE=90°，∠AEB+∠CEF=90°，∴∠BAE=∠CEF，∴△ABE∽△ECF，故③正确；
④中对应边成比例，且夹角均为90°，∴△ABE∽△ECF，故④正确；
⑤中，当
时，则
，即
，
∴
，∴
，∴
，
又∵∠B=∠C=90°，∴△ABE∽△ECF，∴⑤正确；
综上，故选D.
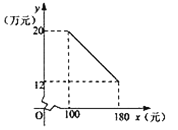
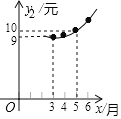
寒假学与练系列答案【题目】2018年非洲猪瘟疫情暴发后，专家预测，2019年我市猪肉售价将逐月上涨，每千克猪肉的售价y1（元）与月份x（1≤x≤12，且x为整数）之间满足一次函数关系，如下表所示．每千克猪肉的成本y2（元）与月份x（1≤x≤12，且x为整数）之间满足二次函数关系，且3月份每千克猪肉的成本全年最低，为9元，如图所示．
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |
（1）求y1与x之间的函数关系式．
（2）求y2与x之间的函数关系式．
（3）设销售每千克猪肉所获得的利润为w（元），求w与x之间的函数关系式，哪个月份销售每千克猪肉所第获得的利润最大？最大利润是多少元？
【题目】为估计某一池塘中鱼的总数目，小英将100尾做了标记的鱼投入池塘中，几天后，随机捕捞，每次捕捞后做好记录，然后将鱼放回，如此进行20次，记录数据如下：
总条数 | 50 | 45 | 60 | 48 | 10 | 30 | 42 | 38 | 15 | 10 |
标记数 | 2 | 1 | 3 | 2 | 0 | 1 | 1 | 2 | 0 | 1 |
总条数 | 53 | 36 | 27 | 34 | 43 | 26 | 18 | 22 | 25 | 47 |
标记数 | 2 | 1 | 2 | 1 | 2 | 1 | 1 | 2 | 1 | 2 |
(1)估计池塘中鱼的总数．根据这种方法估算是否准确?
(2)请设计另一种标记的方法，使得估计更加精准．
