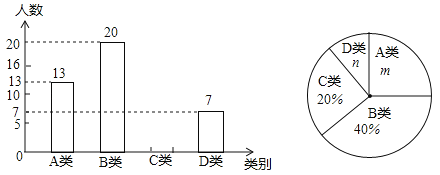
题目内容
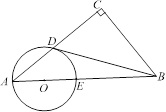
【题目】已知B港口位于A观测点的东北方向,且其到A观测点正北方向的距离BD的长为16千米,一艘货轮从B港口以48千米/时的速度沿如图所示的BC方向航行,15分后到达C处,现测得C处位于A观测点北偏东75°方向,求此时货轮与A观测点之间的距离AC的长(精确大0.1千米)(参考数据:![]() 1.41,
1.41,![]() 1.73,
1.73,![]() 2.24,
2.24,![]() ≈2.45)
≈2.45)
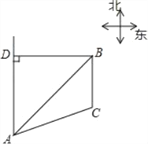
【答案】此时货轮与A观测点之间的距离AC约为15.7km.
【解析】试题分析:根据在Rt△ADB中,sin∠DAB=![]() ,得出AB的长,进而得出tan∠BAH=
,得出AB的长,进而得出tan∠BAH=![]() ,求出BH的长,即可得出AH以及CH的长,进而得出答案.
,求出BH的长,即可得出AH以及CH的长,进而得出答案.
试题解析:
BC=48×![]() =12,
=12,
在Rt△ADB中,sin∠DAB=![]() =
=![]() ,
,
∴AB=![]() =
=![]() ,
,
如图,过点B作BH⊥AC,交AC的延长线于H,

在Rt△AHB中,∠BAH=∠DAC-∠DAB=75°-45°=30°,
tan∠BAH=![]() =
=![]() ,
,
∴AH=![]() BH,
BH,
BH2+AH2=AB2,BH2+(![]() BH)2=(16
BH)2=(16![]() )2,∴BH=8
)2,∴BH=8![]() ,∴AH=8
,∴AH=8![]() ,
,
在Rt△BCH中,BH2+CH2=BC2,∴CH=4,
∴AC=AH-CH=8![]() -4≈15.7km,
-4≈15.7km,
答:此时货轮与A观测点之间的距离AC约为15.7km.

练习册系列答案
相关题目