题目内容
 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第12秒,点E在量角器上对应的读数是
如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第12秒,点E在量角器上对应的读数是考点:圆周角定理
专题:
分析:首先连接OE,由∠ACB=90°,根据圆周角定理,可得点C在⊙O上,即可得∠EOA=2∠ECA,又由∠ECA的度数,继而求得答案.
解答: 解:连接OE,
解:连接OE,
∵∠ACB=90°,
∴点C在以AB为直径的圆上,
即点C在⊙O上,
∴∠EOA=2∠ECA,
∵∠ECA=3×12°=36°,
∴∠AOE=2∠ECA=2×36°=72°.
故答案是:72.
 解:连接OE,
解:连接OE,∵∠ACB=90°,
∴点C在以AB为直径的圆上,
即点C在⊙O上,
∴∠EOA=2∠ECA,
∵∠ECA=3×12°=36°,
∴∠AOE=2∠ECA=2×36°=72°.
故答案是:72.
点评:此题考查了圆周角定理,此题难度适中,解题的关键是证得点C在⊙O上,注意辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
若规定“!”是一种数学运算符号,且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1=24,…,则
的值为( )
| 100! |
| 98! |
A、
| ||
| B、99! | ||
| C、9 900 | ||
| D、2! |
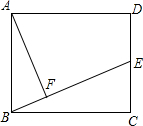 在矩形ABCD中,AB=10,BC=12,E为CD的中点,连接B、E,作AF⊥BE,垂足为F,则AF=
在矩形ABCD中,AB=10,BC=12,E为CD的中点,连接B、E,作AF⊥BE,垂足为F,则AF= 如图所示,点P在数轴上.
如图所示,点P在数轴上. 如图,已知矩形ABCD的边AB=1,BC=3,现把矩形ABCD绕着它的对称中心旋转,若重叠部分的形状为菱形且面积为S,则S的取值范围为
如图,已知矩形ABCD的边AB=1,BC=3,现把矩形ABCD绕着它的对称中心旋转,若重叠部分的形状为菱形且面积为S,则S的取值范围为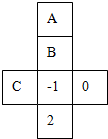 如图是一个正方形盒的展开图,若在其中的三个正方形A、B、C、内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,则填入正方形A、B、C内的三个数依次为多少?
如图是一个正方形盒的展开图,若在其中的三个正方形A、B、C、内分别填入适当的数,使得它们折成正方体后相对的面上的两个数互为相反数,则填入正方形A、B、C内的三个数依次为多少?