Question

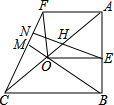如图，在直角梯形ABCF中，AF∥BC，∠ABC=90°，AB=BC，O是对角线AC的中点，OE⊥OF，过点E作EN⊥CF，垂足为N，EN交AC于点H，BO的延长线交CF于点M，则结论：①OE=OF；②OM=OH；③S四边形FOEA=

1

2

S△ABC；④BC=2AF，其中正确结论的个数是（　　）

A．1

B．2

C．3

D．4

Answer 1

分析：求出OA=OB，∠FAO=∠EBO=45°，∠FOA=∠BOE，证△AFO≌△BEO，推出OE=OF，即可判断①，证△FOM≌△EOH，推出OM=OH，即可判断②，求出四边形AFOE面积等于△AOB的面积，即可判断③，根据全等三角形性质求出BE=AF，即可判断④．

解答：解：∵∠ABC=90°，AB=BC，O是对角线AC的中点，
∴AO=OB=CO，∠BAC=∠ABO=∠ACB=45°，BO⊥AC，
∵AF∥BC，∠ABC=90°，
∴∠FAB=90°，
∴∠FAO=45°=∠EBO，
∵OE⊥OF，BO⊥AC，
∴∠FOE=∠AOB=90°，
∴∠FOA=∠BOE=90°-∠AOE，
在△AFO和△BEO中，

∠AOF=∠BOE AO=BO ∠FAO=∠EBO

，
∴△AFO≌△BEO（ASA），
∴OE=OF，∴①正确；
∵EN⊥CF，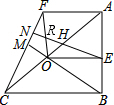
∴∠FNH=∠FOE=90°，
∵∠FRN=∠ERO，∠MFO+∠FNR+∠FRN=180°，∠FOE+∠ORE+∠OER=180°，
∴∠MFO=∠HEO，
∵∠FOE=∠MOA=90°，
∴∠FOM=∠HOE=90°-∠FOH，
在△MFO和△HEO中，

∠MFO=∠HEO OF=OE ∠FOM=∠EOH

∴△MFO≌△HEO（ASA），
∴OM=OH，∴②正确；
∵△AFO≌△BEO，
∴S_{四边形AFOE}=S_△AFO+S_△AOE=S_△BEO+S_△AEO=S_△ABO，
∵AO=CO，BO=BO，
∴S_△ABO=

1

2

AO×BO=

1

2

×

1

2

AC×BO=

1

2

S_△ABC，
即S_{四边形AFOE}=

1

2

S_△ABC，∴③正确；
∵△AFO≌△BEO，
∴AF=BE，
根据已知不能推出AE=BE，
∵AB=BC，
∴不能推出BC=2BE=2AF，∴④错误；
即正确的有3个，
故选C．

点评：本题考查了直角三角形的性质，梯形的性质，三角形的面积，全等三角形的性质和判定的应用，主要考查学生综合运用性质进行推理的能力，有一定的难度．