Question

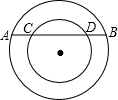如图所示，在两个同心圆中，大圆的弦AB交小圆于C，D，已知AB=2CD，且AB的弦心距等于CD的一半，则大圆与小圆的半径之比为（　　）

• A、

  2

  ：

  5

• B、

  5

  ：

  2

• C、5：2
• D、2：5

Answer 1

分析：同心圆的圆心为O，作OE⊥CD于E，连接0C，OA，用勾股定理求出OC，OA的长，进而得出其比值．

解答：解：作OE⊥CD于E，连接OA，OC，则CE=ED=

1

2

CD，
∵OE=

1

2

CD，∴CE=ED=OE，设OE=R，则EC=R，
∴CO=

2

R，
∵AE=

1

2

AB=CD，∴AE=2R，∴AO=

5

R．
故选B．

点评：此题涉及圆中求半径的问题，此类在圆中涉及弦长、半径、圆心角的计算的问题，常把半弦长，半圆心角，圆心到弦距离转换到同一直角三角形中，然后通过直角三角形予以求解，常见辅助线是过圆心作弦的垂线．