题目内容
14.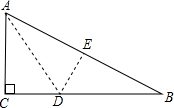 如图,有一块直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD=$\frac{3}{2}$cm.
如图,有一块直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD=$\frac{3}{2}$cm.
分析 先利用勾股定理求得AB=5,然后由翻折的性质得到AE=AC=3,CD=DE,则EB=2,设CD=EC=x,则BD=4-x,然后在Rt△DEB中利用勾股定理列方程求解即可.
解答 解:在Rt△ACB中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
由翻折的性质可知:AE=AC=3,CD=DE,则BE=2.
设CD=DE=x,则BD=4-x.
Rt△DEB中,由勾股定理得:DB2=DE2+EB2,即(4-x)2=x2+22,
解得:x=$\frac{3}{2}$.
∴CD=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$cm.
点评 本题主要考查的是翻折的性质、勾股定理的应用,利用翻折的性质和勾股定理列出关于x的方程是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.随着空气质量的恶化,雾霾天气现象增多,危害加重.森林是“地球之肺”,每年能为人类提供大约28.3亿吨的有机物,28.3亿可用科学记数法表示为( )
| A. | 28.3×108 | B. | 2.83×109 | C. | 2.83×10 | D. | 2.83×107 |
2.下列多项式能分解因式的是( )
| A. | x2-y | B. | x2+1 | C. | x2+2xy+4y2 | D. | x2+4x+4 |
6.规定一种运算:a*b=ab+a-b,其中a和b是有理数,那么-3*5的值为( )
| A. | 7 | B. | -23 | C. | -17 | D. | -13 |
4.“十、一”黄金周期间,张掖丹霞在7天假期中每天接待游客的人数变化如表(正数表示比前一天多的人数,负数表示比前一天少的人数)
(1)若9月30日的游客人数记为a万人,请用代数式表示10月2日的游客人数?
(2)请判断七天内游客人数最多的是哪天?
(3)若9月30日的游客人数为2万人,门票每人60元.问黄金周期间张掖丹霞门票收入是多少元?(用科学计算法表示)
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 10月7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)请判断七天内游客人数最多的是哪天?
(3)若9月30日的游客人数为2万人,门票每人60元.问黄金周期间张掖丹霞门票收入是多少元?(用科学计算法表示)

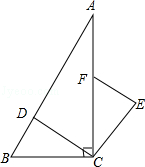 如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.