题目内容
 (2012•河东区一模)某中学对全校学生60秒跳绳的次数进行了统计,全校平均次数是100次.某班体育委员统计了全班50名学生60秒跳绳的成绩,列出的频数分布直方图如下(每个分组包括左端点,不包括右端点):
(2012•河东区一模)某中学对全校学生60秒跳绳的次数进行了统计,全校平均次数是100次.某班体育委员统计了全班50名学生60秒跳绳的成绩,列出的频数分布直方图如下(每个分组包括左端点,不包括右端点):(Ⅰ)求该班60秒跳绳的平均次数是多少?
(Ⅱ)从该班中任选一人,其跳绳次数达到或超过校平均次数的概率是多少?
分析:(1)根据频率分布直方图,先求出该班50个人跳绳次数的总和,再除以50就可以求出平均次数;
(2)根据频率分布直方图,先求出达到或超过校平均次数100次的次数之和,再除以50即可求出概率.
(2)根据频率分布直方图,先求出达到或超过校平均次数100次的次数之和,再除以50即可求出概率.
解答:解:(Ⅰ)该班60秒跳绳的平均次数是:
=110.8;
(Ⅱ)该班60秒跳绳成绩大于或等于100次的有:19+7+5+2=33(人),
=0.66,
所以,从该班任选一人,跳绳成绩达到或超过校平均次数的概率为0.66.
| 70×4+90×13+110×19+130×7+150×5+170×2 |
| 50 |
(Ⅱ)该班60秒跳绳成绩大于或等于100次的有:19+7+5+2=33(人),
| 33 |
| 50 |
所以,从该班任选一人,跳绳成绩达到或超过校平均次数的概率为0.66.
点评:本题考查了频率分布直方图,解题的关键是能根据频率直方图得出相关数据,并能找出等量关系.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
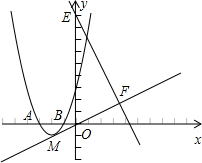 (Ⅰ)求抛物线C的解析式;
(Ⅰ)求抛物线C的解析式;