题目内容
图a是一个三角形,分别连接这个三角形三边的中点得到图b;再分别连接图b中间小三角形的三边的中点,得到图c

(1)图b有______个三角形,图c有______个三角形.
(2)按上面的方法继续下去,第n个图形中有多少个三角形(用n的代数式表示结论).
(3)当n=10时,第10个图形中有多少个三角形?
解:(1)b中有5个三角形,c中有9个三角形.
(2)依题意得:n=1时,有1个三角形;
n=2时,有5个三角形;
n=3时,有9个三角形;
…
∴当n=n时有4n-3个三角形.
(3)当n=10时,有40-3=37个三角形.
分析:(1)可直接通过图形写出三角形的个数;
(2)本题可分别写出n=1,2,3…时所对应的三角形个数,找出有关于n的代数式;
(3)将n=10代入(2)中代数式即可.
点评:本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.
(2)依题意得:n=1时,有1个三角形;
n=2时,有5个三角形;
n=3时,有9个三角形;
…
∴当n=n时有4n-3个三角形.
(3)当n=10时,有40-3=37个三角形.
分析:(1)可直接通过图形写出三角形的个数;
(2)本题可分别写出n=1,2,3…时所对应的三角形个数,找出有关于n的代数式;
(3)将n=10代入(2)中代数式即可.
点评:本题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.

练习册系列答案
相关题目
(本题共4分)图1是一个三角形,分别连接这个三角形三边的中点得到图②;再分别连接图②中间小三角形三边的中点,得到图③.
|
|
|
⑴图②有_____个三角形;图③有_____个三角形.
⑵按上面的方法继续下去,第![]() 个图形中有多少个三角形?(用含有
个图形中有多少个三角形?(用含有![]() 的式子表示结论)数值。
的式子表示结论)数值。
(本题共4分)图1是一个三角形,分别连接这个三角形三边的中点得到图②;再分别连接图②中间小三角形三边的中点,得到图③.


|
|
|
⑴图②有_____个三角形;图③有_____个三角形.
⑵按上面的方法继续下去,第
 个图形中有多少个三角形?(用含有
个图形中有多少个三角形?(用含有 的式子表示结论)数值。
的式子表示结论)数值。 (本题共4分)图1是一个三角形,分别连接这个三角形三边的中点得到图②;再分别连接图②中间小三角形三边的中点,得到图③.



|
|
|
⑴图②有_____个三角形;图③有_____个三角形.
⑵按上面的方法继续下去,第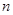 个图形中有多少个三角形?(用含有
个图形中有多少个三角形?(用含有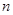 的式子表示结论)数值。
的式子表示结论)数值。



