题目内容
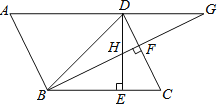
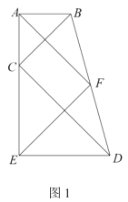
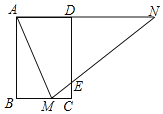
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() 点
点![]() 在直线
在直线![]() 上,
上,![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() 是等腰三角形;
是等腰三角形;
(2)求证:![]() ;
;
(3)当![]() 为
为![]() 中点时,求
中点时,求![]() 的长.
的长.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)由矩形的性质得出AD∥BC,由平行线的性质得出∠NAM=∠BMA,由已知∠AMN=∠AMB,得出∠AMN=∠NAM,即可得出结论;
(2)由矩形的性质得出AD∥BC,AD=BC=2,AB=CD=3,由平行线的性质得出∠NAM=∠BMA,作NH⊥AM于H,由等腰三角形的性质得出AH=![]() AM,证明△NAH∽△AMB,得出
AM,证明△NAH∽△AMB,得出![]() ,即可得出结论;
,即可得出结论;
(3)求出BM=CM=![]() BC=
BC=![]() ×2=1,由(2)得AM2=2BMAN,得出AM2=2AN,由勾股定理得出AM2=AB2+BM2=10,求出AN=5,得出DN=AN-AD=3,设DE=x,则CE=3-x,证明△DNE∽△CME,得出
×2=1,由(2)得AM2=2BMAN,得出AM2=2AN,由勾股定理得出AM2=AB2+BM2=10,求出AN=5,得出DN=AN-AD=3,设DE=x,则CE=3-x,证明△DNE∽△CME,得出![]() ,求出DE=
,求出DE=![]() ,得出CE=DC-DE=
,得出CE=DC-DE=![]() ,再由勾股定理即可得出答案.
,再由勾股定理即可得出答案.
解:(1)证明:∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() 是等腰三角形;
是等腰三角形;
(2)解:作![]() 于
于![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
(3)解:∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
由(2)得,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
解得,![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() .
.


练习册系列答案
相关题目