题目内容
 (2012•瑶海区一模)为加快城市跨越式发展,某城市规划部门准备在某河两岸假设一座桥梁,AB是该河北岸一段,长为3千米,C为南岸一渡口,为了解决两岸交通困难,拟在渡口C处架桥.经测量得A在C北偏西30°方向,B在C的东北方向,从C处连接两岸最短的桥长多少米?
(2012•瑶海区一模)为加快城市跨越式发展,某城市规划部门准备在某河两岸假设一座桥梁,AB是该河北岸一段,长为3千米,C为南岸一渡口,为了解决两岸交通困难,拟在渡口C处架桥.经测量得A在C北偏西30°方向,B在C的东北方向,从C处连接两岸最短的桥长多少米?分析:首先过点C作CD⊥AB于点D,则CD就是连接两岸最短的桥,然后设CD=x千米,利用三角函数可得BD=x千米,AD=
x千米,则可得方程:x+
x=3,解此方程即可求得答案.
| ||
| 3 |
| ||
| 3 |
解答: 解:过点C作CD⊥AB于点D,则CD就是连接两岸最短的桥.
解:过点C作CD⊥AB于点D,则CD就是连接两岸最短的桥.
设CD=x千米,
∵在Rt△BCD中,∠BCD=45°,
∴BD=CD=x(千米),
∵在Rt△ACD中,∠ACD=30°,
∴AD=CD•tan∠ACD=
x(千米),
∵AD+DB=AB,
∴x+
x=3,
解得:x=
≈1.9.
答:从C处连接两岸最短的桥长为1.9千米.
 解:过点C作CD⊥AB于点D,则CD就是连接两岸最短的桥.
解:过点C作CD⊥AB于点D,则CD就是连接两岸最短的桥.设CD=x千米,
∵在Rt△BCD中,∠BCD=45°,
∴BD=CD=x(千米),
∵在Rt△ACD中,∠ACD=30°,
∴AD=CD•tan∠ACD=
| ||
| 3 |
∵AD+DB=AB,
∴x+
| ||
| 3 |
解得:x=
9-3
| ||
| 2 |
答:从C处连接两岸最短的桥长为1.9千米.
点评:此题考查了方向角问题.此题难度不大,解题的关键是构造直角三角形,并利用解直角三角形的性质求解.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
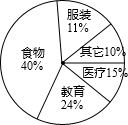 (2012•瑶海区一模)在春节期间,小明对自己家7天的家庭开支情况进行了统计,各类支出如图所示,用于食物费用为800元,那么本月用于教育的费用为( )
(2012•瑶海区一模)在春节期间,小明对自己家7天的家庭开支情况进行了统计,各类支出如图所示,用于食物费用为800元,那么本月用于教育的费用为( )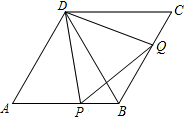 (2012•瑶海区一模)在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.试判断△PDQ的形状,并证明.
(2012•瑶海区一模)在菱形ABCD中,∠A=60°,点P、Q分别在边AB、BC上,且AP=BQ.试判断△PDQ的形状,并证明.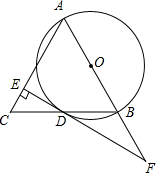 (2012•瑶海区一模)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
(2012•瑶海区一模)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.