题目内容
如图,在湖滨公园内,有一个游船码头O.已知游船A在码头O的北偏东30°方向,游船B在游船A的正南方向,OA=60米,OB=20 米.
米.(1)请计算说明:游船B在游船码头O的什么方向?
(2)求两游船A、B之间的距离.

【答案】分析:(1)过O作OC垂直于AB交AB的延长线于C,根据已知利用三角函数求得OC的长.已知OB的长,利用三角函数可以求得∠BOC的度数,即求得了B在港口O的方向.
(2)在(1)的基础上,利用三角函数解直角三角形即可解答.
解答: 解:过O作OC⊥AB,交AB的延长线于C.
解:过O作OC⊥AB,交AB的延长线于C.
(1)在Rt△AOC中,
∵∠AOC=60°,
∴cos60°= ,
,
∴OC= OA=
OA= ×60=30(海里),
×60=30(海里),
在Rt△OBC中,
∵cos∠BOC= =
= =
= ,
,
∴∠BOC=30°.
∴小岛B在港口O的北偏东60°(答东偏北30°亦可).
(2)由(1)知∠AOB=∠BAO=30°,
所以AB=OB=20 (海里).
(海里).
答:两小岛A,B的距离为20 海里.
海里.
点评:此题主要考查了方向角问题的应用,培养学生对方向角的掌握及运用的能力,难易程度适中.
(2)在(1)的基础上,利用三角函数解直角三角形即可解答.
解答:
 解:过O作OC⊥AB,交AB的延长线于C.
解:过O作OC⊥AB,交AB的延长线于C.(1)在Rt△AOC中,
∵∠AOC=60°,
∴cos60°=
 ,
,∴OC=
 OA=
OA= ×60=30(海里),
×60=30(海里),在Rt△OBC中,
∵cos∠BOC=
 =
= =
= ,
,∴∠BOC=30°.
∴小岛B在港口O的北偏东60°(答东偏北30°亦可).
(2)由(1)知∠AOB=∠BAO=30°,
所以AB=OB=20
 (海里).
(海里).答:两小岛A,B的距离为20
 海里.
海里.点评:此题主要考查了方向角问题的应用,培养学生对方向角的掌握及运用的能力,难易程度适中.

练习册系列答案
相关题目
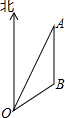 如图,在湖滨公园内,有一个游船码头O.已知游船A在码头O的北偏东30°方向,游船B在游船A的正南方向,OA=60米,OB=20
如图,在湖滨公园内,有一个游船码头O.已知游船A在码头O的北偏东30°方向,游船B在游船A的正南方向,OA=60米,OB=20 如图,在湖滨公园内,有一个游船码头O.已知游船A在码头O的北偏东30°方向,游船B在游船A的正南方向,OA=60米,OB=20
如图,在湖滨公园内,有一个游船码头O.已知游船A在码头O的北偏东30°方向,游船B在游船A的正南方向,OA=60米,OB=20 米.
米.