Question

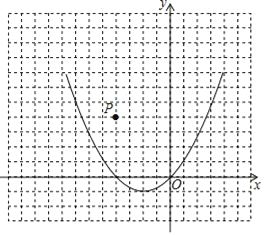
【题目】已知二次函数y=x2+x的图象，如图所示．

（1）在同一直角坐标系中用描点法画出一次函数y=x+的图象，观察图象写出自变量x取值在什么范围时，一次函数的值小于二次函数的值；

（2）如图，点P是坐标平面上的一点，并在网格的格点上，请选择一种适当的平移方法，使平移后二次函数图象的顶点落在P点上，写出平移后二次函数图象的函数表达式，并判断点P是否在函数y=x+的图象上，请说明理由．

Answer 1

【答案】（1）当x＜﹣1.5或x＞1时，一次函数的值小于二次函数的值；（2）点P在直线y=x+的函数图象上．

【解析】试题分析：

（1）由题意和图可知，小正方形的边长为0.5个单位长度，这样先求得直线上任意两点的坐标，根据坐标在图中描出这两个点，然后画出过这两点的直线即可得到直线y=x+的函数图象，然后找出一次函数图象位于抛物线下方部分x的取值范围即可；

（2）先依据抛物线的顶点坐标和点P的坐标，确定出抛物线移动的方向和距离，然后依据抛物线的顶点式写出抛物线的解析式即可，将点P的坐标代入函数解析式，如果点P的坐标符合函数解析式，则点P在直线上，否则点P不在直线上．

试题解析：

（1）∵将x=0代入y=x+得y=，将x=1代入得：y=2，

∴直线y=x+经过点（0， ），（1，2）．

由抛物线y=x2+x与x轴左侧交点的位置可知，图中小正方形的边长为0.5个单位长度，由此可画出直线y=x+的图象如下图所示：

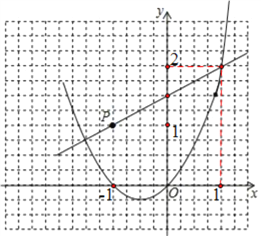
由函数图象可知：当x＜﹣1.5或x＞1时，一次函数的值小于二次函数的值．

（2）由抛物线y=x2+x=(x+)2-可知，抛物线的顶点坐标为（， ），点P的坐标为（-1，1），

∴先将抛物线向上平移个单位，再向左平移个单位，即可使平移后的抛物线顶点落在点P（﹣1，1）处．

∴平移后的二次函数的表达式为：y=（x+1）2+1，即：y=x2+2x+2；

点P在y=x+的函数图象上．理由如下：

∵把x=﹣1代入y=x+得：y=1，

∴点P的坐标符合直线的解析式．

∴点P在直线y=x+的函数图象上．