题目内容
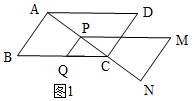
【题目】如图1所示，在ABCD中，AB=3cm，BC=5cm，AC⊥AB，△ACD沿射线AC的方向匀速平移得到△PNM，速度为1cm/s，同时，点Q从点C出发，沿射线CB方向匀速运动，速度为1cm/s，当△PNM停止平移时，点Q也停止运动，如图2所示，设运动时间为t（s）（0＜t＜4）．
（1）当t为何值时，PQ∥MN？
（2）设△QMC的面积为y（cm2），求y与t之间的函数关系式；
（3）是否存在某一时刻t，使得PQ=QM，若存在，求出t的值；若不存在，请说明理由．
【答案】
（1）
解：如图1，由题意得：CQ=AP=t，
在Rt△ABC中，由勾股定理得AC= 
= 
=4，
∴CP=4﹣t，
由平移的性质可得MN∥AB，
∵PQ∥MN，
∴PQ∥AB，
∴ 
，即 
，
解得t= 
，
则当t为何值时，PQ∥MN
（2）
解：如图2，过点P作PF⊥BC于点F，过点A作AE⊥BC于点E，
由S△ABC= 
AB×AC= AE×BC，
×3×4= ×5AE，
可得：AE= 
，
则由勾股定理易得：CE= 
= 
= 
．
∵PD⊥BC，AE⊥BC，
∴AE∥PD，
∴△CPD∽△CAE，
∴ 
，即 
∴PD= 
，CD= 
，
∵PM∥BC，
∴点M到BC的距离h=PD= ，
∴△QCM的面积y= CQ×h= × 
=﹣ 
+ 
（0＜t＜4）
（3）
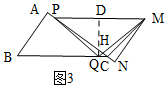
解：如图3，过点Q作QD⊥PM于点D，QD交AC于点H．
∵PQ=MQ，
∴PD=DM= 
，且DQ⊥BC．
在Rt△ABC中，AC=4，AP=t，QC=t．
∵∠A=∠HQC，∠ACB=∠QCH，
∴△CQH∽△CAB，
∴ 
，即 
，
∴CH= 
t，
∴PH=AC﹣AP﹣CH=4﹣t﹣ t=4﹣ 
t，
易证△PHD∽△CBA，
∴ 
，
即 
，
解得t= 
．
∴当t= 时，PQ=QM．
【解析】（1）如图1，先根据题意得：CQ=AP=t，利用勾股定理求AC的长，根据PQ∥AB，列比例式可求得t的值；（2）如图2，作辅助线，构建相似三角形，利用面积法得：S△ABC= AB×AC= AE×BC，可得：AE= ，由勾股定理易得：CE= ．证明△CPD∽△CAE，列比例式 ，求PD和CD的长，根据面积公式求△QCM的面积y；（3）如图3，作辅助线，构建相似三角形，证明△CQH∽△CAB，列比例式得： ，表示CH= t，则PH=AC﹣AP﹣CH=4﹣ t，易证△PHD∽△CBA，列式可求得t的值．
【考点精析】利用勾股定理的概念和平行四边形的性质对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分．
