题目内容
设a,b,c是△ABC的三边长,二次函数 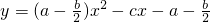 (其中2a≠b),
(其中2a≠b),
(1)当b=2a+8c时,求二次函数的对称轴;
(2)当x=1时,二次函数最小值为 b,试判断△ABC的形状,并说明理由.
b,试判断△ABC的形状,并说明理由.
解:(1)根据二次函数对称轴的公式,得
x=-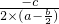 =
=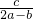 =
=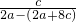 =-
=- ;
;
(2)根据题意可知
-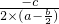 =1,
=1,
化简得
c=2a-b①,
把x=1代入函数解析式,可得
a- -c-a-
-c-a- =-
=- b,
b,
即c= b②,
b②,
把②代入①,得
a= b,
b,
∴a2+c2= b2+
b2+ b2=b2,
b2=b2,
∴△ABC是以b为斜边的直角三角形.
分析:(1)直接根据函数解析式,代入对称轴的公式,在计算过程中,注意把b=2a+8c代入即可;
(2)根据题意可知对称轴是x=1,于是-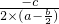 =1,化简得c=2a-b,然后把x=1代入二次函数解析式可得c=
=1,化简得c=2a-b,然后把x=1代入二次函数解析式可得c= b,把c=
b,把c= b代入c=2a-b中可得a=
b代入c=2a-b中可得a= b,计算可得a2+c2=b2,根据勾股定理的逆定理可知△ABC是直角三角形.
b,计算可得a2+c2=b2,根据勾股定理的逆定理可知△ABC是直角三角形.
点评:本题考查了二次函数性质、二次函数最值,解题的关键是区分公式中a、b、c与三角形三边a、b、c的不同,灵活使用勾股定理逆定理.
x=-
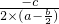 =
=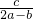 =
=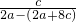 =-
=- ;
;(2)根据题意可知
-
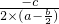 =1,
=1,化简得
c=2a-b①,
把x=1代入函数解析式,可得
a-
 -c-a-
-c-a- =-
=- b,
b,即c=
 b②,
b②,把②代入①,得
a=
 b,
b,∴a2+c2=
 b2+
b2+ b2=b2,
b2=b2,∴△ABC是以b为斜边的直角三角形.
分析:(1)直接根据函数解析式,代入对称轴的公式,在计算过程中,注意把b=2a+8c代入即可;
(2)根据题意可知对称轴是x=1,于是-
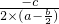 =1,化简得c=2a-b,然后把x=1代入二次函数解析式可得c=
=1,化简得c=2a-b,然后把x=1代入二次函数解析式可得c= b,把c=
b,把c= b代入c=2a-b中可得a=
b代入c=2a-b中可得a= b,计算可得a2+c2=b2,根据勾股定理的逆定理可知△ABC是直角三角形.
b,计算可得a2+c2=b2,根据勾股定理的逆定理可知△ABC是直角三角形.点评:本题考查了二次函数性质、二次函数最值,解题的关键是区分公式中a、b、c与三角形三边a、b、c的不同,灵活使用勾股定理逆定理.

练习册系列答案
相关题目
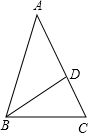 如图,在△ABC中,∠A=36°,AB=AC,BD是∠ABC的平分线,设CD=a,BD=b,AB=c.
如图,在△ABC中,∠A=36°,AB=AC,BD是∠ABC的平分线,设CD=a,BD=b,AB=c.
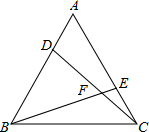 如图,在等边三角形ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过t分钟后,它们分别爬行到了D、E处,设DC与BE的交点为F.
如图,在等边三角形ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以相同的速度由A向B和由C向A爬行,经过t分钟后,它们分别爬行到了D、E处,设DC与BE的交点为F.