题目内容

已知：⊙O与⊙O₁外切于C，P是⊙O上任一点，PT与⊙O₁相切于点T．求证：PC：PT是定值．

证明：如图所示，⊙O₁，⊙O，两圆半径分别为R、r．
延长PC与圆交于E点，连接O₁E，PO，OO₁，
∵OP=OC，O₁C=O₁E，
∴∠OCP=∠OPC，∠O₁CE=∠O₁EC．
又∵∠OCP与∠O₁CE是对顶角，
∴∠OCP=∠O₁CE，
∴∠OCP=∠OPC=∠O₁CE=∠O₁EC，
∴△OCP∽△O₁CE，
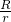∴ $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ，即CE= $\text{[math]}$ PC．
∵PT与⊙O₁相切于点T，
∴PT²=PC•PE=PC•（PC+CE）=PC•（PC+ 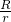$\text{[math]}$ PC），
即PT²=PC²（1+ $\text{[math]}$ ），
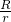∴PC：PT= $\text{[math]}$ ．为定值．
分析：要证PC：PT是定值，如图证明△OCP与△O₁CE相似，则CE可以用PC来表示得CE= 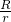$\text{[math]}$ PC，再由PT与⊙O₁相切于点T，可得PT²=PC•PE，代换后可得PT²=PC²（1+ 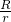$\text{[math]}$ ），进而得PC：PT为定值．
点评：本题考查了相切圆的性质与相似三角形的判定和性质，同学们应熟练掌握．