题目内容
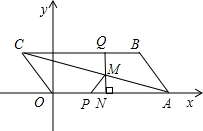
如图所示,在直角坐标系中,?ABCO的点A(4,0)、B(3,2).点P从点O出发,以2单位/秒的速度向点A运动,同时点Q由点B出发,以1单位/秒的速度向点C运动,当其中一点到达终点时,另一点也随之停止.过点Q作QN⊥x轴于点N,连接AC交NQ于点M,连接PM.设动点Q运动的时间为t秒(1)点C的坐标为
(2)点M的坐标为
(3)求△PMA的面积S与时间t的函数关系式;是否存在t的值,使△PMA的面积最大?若存在,求出t的值;
 若不存在,请说明理由.
若不存在,请说明理由.
分析:(1)由于四边形ABCO是平行四边形,CB=OA,C与B等高,故C点坐标可以求出.
(2)点M横坐标为(3-t),又
=
,求得M点纵坐标.
(3)由求得的M点坐标可求得△PMA的面积S=
•PA•MN,列出函数关系式,求得最大值.
(2)点M横坐标为(3-t),又
| AN |
| CQ |
| NM |
| MQ |
(3)由求得的M点坐标可求得△PMA的面积S=
| 1 |
| 2 |
解答:解:(1)C(-1,2)
(2)M(3-t,
)
(3)∵点P速度第秒2个单位,
∴QP=2t,AP=4-2t;
∴S=
AP•MN=
(4-2t)
=-
(t2-t-2)=-
(t-
)2+
,
∴当t=
时,S有最大值为
.
(2)M(3-t,
| 2+2t |
| 5 |
(3)∵点P速度第秒2个单位,
∴QP=2t,AP=4-2t;
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2+2t |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 1 |
| 2 |
| 9 |
| 10 |
∴当t=
| 1 |
| 2 |
| 9 |
| 10 |
点评:本题考查了通过动点运动列出函数关系式,并求得最值,综合性强.

练习册系列答案
相关题目
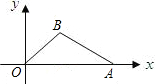 sin∠BOA=
sin∠BOA= 1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.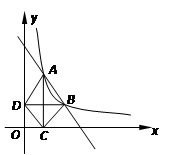

 的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.