题目内容
(1)计算: +
+ ;
;
(2)已知a= ,求(
,求( )÷a的值;
)÷a的值;
(3)解方程:x2-4x+1=0;
(4)解方程:(x-1)2-3(x-1)=0.
解:(1)原式=7 -5
-5 +3
+3 =5
=5 ;
;
(2)( )÷a=
)÷a=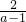
 =
= ,
,
把a= 代入得:
代入得:
原式= =
= ;
;
(3)∵a=1,b=-4,c=1
∴b2-4ac=12
∴x= =
= ,
,
∴x1=2+ ,x2=2-
,x2=2- .
.
(4)(x-1)2-3(x-1)=0.
(x-1)[(x-1)-3]=0
(x-1)(x-4)=0
x-1=0或x-4=0
x1=1,x2=4;
分析:(1)先将二次根式化为最简,然后合并同类项即可得出答案.
(2)先把要求的式子进行化简,再把a的值代入即可求出答案.
(3)先根据方程确定二次项系数,一次项系数,常数项,即a=1,b=4,c=-1,再代入求根公式即可.
(4)提取公因式x-1,再根据“两式相乘为0,则至少有一个式子值为0”解方程.
点评:此题考查了二次根式的加减和解题一元二次方程,用到的知识点是用公式法和因式分解法解一元二次方程、二次根式的化简求值等,要牢记求根公式注意:先把方程化为一般形式ax2+bx+c=0后,再确定a,b,c的值.
 -5
-5 +3
+3 =5
=5 ;
;(2)(
 )÷a=
)÷a=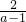
 =
= ,
,把a=
 代入得:
代入得:原式=
 =
= ;
;(3)∵a=1,b=-4,c=1
∴b2-4ac=12
∴x=
 =
= ,
,∴x1=2+
 ,x2=2-
,x2=2- .
.(4)(x-1)2-3(x-1)=0.
(x-1)[(x-1)-3]=0
(x-1)(x-4)=0
x-1=0或x-4=0
x1=1,x2=4;
分析:(1)先将二次根式化为最简,然后合并同类项即可得出答案.
(2)先把要求的式子进行化简,再把a的值代入即可求出答案.
(3)先根据方程确定二次项系数,一次项系数,常数项,即a=1,b=4,c=-1,再代入求根公式即可.
(4)提取公因式x-1,再根据“两式相乘为0,则至少有一个式子值为0”解方程.
点评:此题考查了二次根式的加减和解题一元二次方程,用到的知识点是用公式法和因式分解法解一元二次方程、二次根式的化简求值等,要牢记求根公式注意:先把方程化为一般形式ax2+bx+c=0后,再确定a,b,c的值.

练习册系列答案
相关题目
