题目内容
【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y= ![]() (k≠0)的图象恰好经过点A′,B,则k的值为 .
(k≠0)的图象恰好经过点A′,B,则k的值为 . 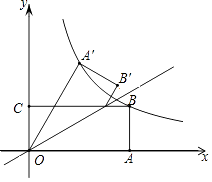
【答案】![]()
【解析】解:∵四边形ABCO是矩形,AB=1,
∴设B(m,1),
∴OA=BC=m,
∵四边形OA′B′D与四边形OABD关于直线OD对称,
∴OA′=OA=m,∠A′OD=∠AOD=30°,
∴∠A′OA=60°,
过A′作A′E⊥OA于E,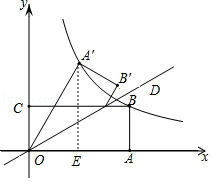
∴OE= ![]() m,A′E=
m,A′E= ![]() m,
m,
∴A′( ![]() m,
m, ![]() m),
m),
∵反比例函数y= ![]() (k≠0)的图象恰好经过点A′,B,
(k≠0)的图象恰好经过点A′,B,
∴ ![]() m
m ![]() m=m,
m=m,
∴m= ![]() ,
,
∴k= ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等.

练习册系列答案
相关题目