题目内容

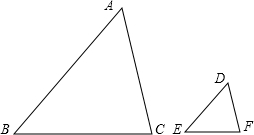教材第97页在证明“两边对应成比例且夹角对应相等的两个三角形相似”（如图，已知

（AB＞DE），∠A=∠D，求证：△ABC∽△DEF）时，利用了转化的数学思想，通过添设辅助线，将未知的判定方法转化为前两节课已经解决的方法（即已知两组角对应相等推得相似或已知平行推得相似）．请利用上述方法完成这个定理的证明．

分析：在AB上截取AG=DE，作GH∥BC，则可得△AGH∽△ABC，再由已知条件证明△AGH≌△DEF即可证明：△ABC∽△DEF．

解答：证明：在AB上截取AG=DE，作GH∥BC，
∴△AGH∽△ABC，
∴

，

∵

，AG=DE，
∴AH=DF，
∵∠A=∠D，
∴△AGH≌△DEF，
∴△ABC∽△DEF．

点评：本题考查了相似三角形的判定和性质以及全等三角形的判定，解题的关键是正确作出辅助线构造全等三角形．

练习册系列答案

好帮手全程测控系列答案

教材第97页在证明“两边对应成比例且夹角对应相等的两个三角形相似”（如图，已知 $数学公式$ （AB＞DE），∠A=∠D，求证：△ABC∽△DEF）时，利用了转化的数学思想，通过添设辅助线，将未知的判定方法转化为前两节课已经解决的方法（即已知两组角对应相等推得相似或已知平行推得相似）．请利用上述方法完成这个定理的证明．

试题分类