题目内容
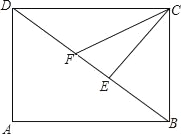
【题目】如图,正方形ABCD中,AB=![]() ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF.
,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE,CF.

(1)若A,E,O三点共线,求CF的长;
(2)求△CDF的面积的最小值.
【答案】(1)CF=3;(2)![]() .
.
【解析】
(1)由正方形的性质可得AB=BC=AD=CD=2![]() ,根据勾股定理可求AO=5,即AE=3,由旋转的性质可得DE=DF,∠EDF=90°,根据“SAS”可证△ADE≌△CDF,可得AE=CF=3;
,根据勾股定理可求AO=5,即AE=3,由旋转的性质可得DE=DF,∠EDF=90°,根据“SAS”可证△ADE≌△CDF,可得AE=CF=3;
(2)由△ADE≌△CDF,可得S△ADE=S△CDF,当OE⊥AD时,S△ADE的值最小,即可求△CDF的面积的最小值.
(1)由旋转得:![]() ,
,![]() ,
,
∵![]() 是
是![]() 边的中点,
边的中点,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中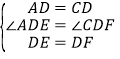 ,
,
∴![]() ,
,
∴![]() ;
;
(2)由于![]() ,所以
,所以![]() 点可以看作是以
点可以看作是以![]() 为圆心,2为半径的半圆上运动,
为圆心,2为半径的半圆上运动,
过点![]() 作
作![]() 于点
于点![]() ,
,
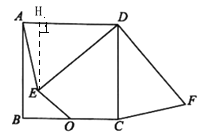
∵![]() ,
,
∴![]() ,
,
当![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() 最小,
最小,![]() ,
,
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目