题目内容
 如图所示,每个小正方形的边长均为1,则下列A、B、C、D四个图中的三角形(阴影部分)与△EFG相似的是( )
如图所示,每个小正方形的边长均为1,则下列A、B、C、D四个图中的三角形(阴影部分)与△EFG相似的是( )分析:根据相似三角形的判定,易得出△ABC的三边的边长,故只需分别求出各选项中三角形的边长,分析两三角形对应边是否成比例即可.
解答:解:∵小正方形的边长为1,
∴在△ABC中,EG=
,FG=2,EF=
=
,
A中,一边=3,一边=
,一边=
=
,三边与△ABC中的三边不能对应成比例,故两三角形不相似.故A错误;
B中,一边=1,一边=
,一边=
=
,
有
=
=
,即三边与△ABC中的三边对应成比例,故两三角形相似.故B正确;
C中,一边=1,一边=
,一边=2
,三边与△ABC中的三边不能对应成比例,故两三角形不相似.故C错误;
D中,一边=2,一边=
,一边=
=
,三边与△ABC中的三边不能对应成比例,故两三角形不相似.故D错误.
故选:B.
∴在△ABC中,EG=
| 2 |
| 1+32 |
| 10 |
A中,一边=3,一边=
| 2 |
| 1+22 |
| 5 |
B中,一边=1,一边=
| 2 |
| 22+1 |
| 5 |
有
| ||
| 1 |
| 2 | ||
|
| ||
|
C中,一边=1,一边=
| 5 |
| 2 |
D中,一边=2,一边=
| 5 |
| 32+22 |
| 13 |
故选:B.
点评:本题考查了相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.本题中把若干线段的长度用同一线段来表示是求线段是否成比例时常用的方法.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
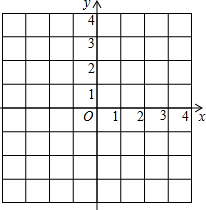 如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现:
如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现: 如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现:
如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现: