题目内容
如图，平行四边形ABCD在平面直角坐标系中，AD=6．若OA、OB的长是关于x的一元二次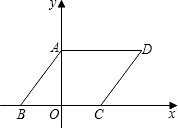
方程x2-7x+12=0的两个根，且OA＞OB；
（1）求sin∠ABC的值；
（2）若E为x轴上的点，且S△AOE=
，求出点E的坐标，并判断△AOE与△DAO是否相似？请说明理由．
方程x2-7x+12=0的两个根，且OA＞OB；（1）求sin∠ABC的值；
（2）若E为x轴上的点，且S△AOE=
| 16 |
| 3 |
（1）解方程：x2-7x+12=0
解得x1=3，x2=4（1分）
∵OA＞OB
∴OA=4，OB=3（2分）
由勾股定理得出：
∴AB=5（3分）
∴在Rt△OAB中，sin∠ABC=
=
（4分）
（2）①∵S△AOE=
∴
OA•OE=
∴OE=
（5分）
∴点E的坐标为（-
，0）或（
，0）（6分）
②△AOE与△DAO相似，理由如下：
∵
=
，
=
∴
=
∵∠AOE=∠DAO=90°（7分）
∴△AOE∽△DAO．（8分）
解得x1=3，x2=4（1分）
∵OA＞OB
∴OA=4，OB=3（2分）
由勾股定理得出：
∴AB=5（3分）
∴在Rt△OAB中，sin∠ABC=
| OA |
| AB |
| 4 |
| 5 |
（2）①∵S△AOE=
| 16 |
| 3 |
∴
| 1 |
| 2 |
| 16 |
| 3 |
∴OE=
| 8 |
| 3 |
∴点E的坐标为（-
| 8 |
| 3 |
| 8 |
| 3 |
②△AOE与△DAO相似，理由如下：
∵
| OE |
| OA |
| 2 |
| 3 |
| OA |
| AD |
| 2 |
| 3 |
∴
| OE |
| OA |
| OA |
| AD |
∵∠AOE=∠DAO=90°（7分）
∴△AOE∽△DAO．（8分）
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
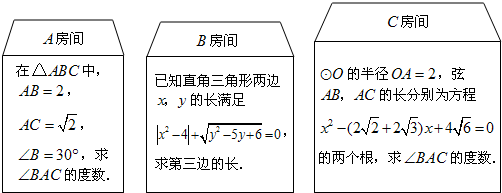
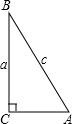
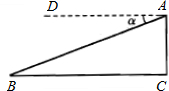的俯角α=20°（B、C在同一水平线上），求目标C到控制点B的距离（精确到1米）．
