Question

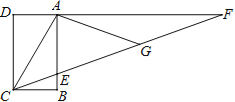
【题目】如图，AB是⊙O的直径，C、G是⊙O上两点，且AC=CG，过点C的直线CD⊥BG于点D，交BA的延长线于点E，连接BC，交OD于点F．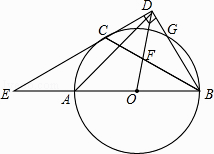
（1）求证：CD是⊙O的切线．
（2）若 ，求∠E的度数．
（3）连接AD，在（2）的条件下，若CD= ，求AD的长．

Answer 1

【答案】
（1）证明：如图1，连接OC，AC，CG，

∵AC=CG，

∴ ，

∴∠ABC=∠CBG，

∵OC=OB，

∴∠OCB=∠OBC，

∴∠OCB=∠CBG，

∴OC//BG，

∵CD⊥BG，

∴OC⊥CD，

∴CD是⊙O的切线；

（2）解：∵OC//BD，

∴△OCF∽△BDF，△EOC∽△EBD，

∴ ，

∴ ，

∵OA=OB，

∴AE=OA=OB，

∴OC= OE，

∵∠ECO=90°，

∴∠E=30°

（3）解：如图2，过A作AH⊥DE于H，

∵∠E=30°

∴∠EBD=60°，

∴∠CBD= EBD=30°，

∵CD= ，

∴BD=3，DE=3 ，BE=6，

∴AE= BE=2，

∴AH=1，

∴EH= ，

∴DH=2 ，

在Rt△DAH中，AD= = = ．

【解析】（1）如图1，连接OC，AC，CG，由圆周角定理得到∠ABC=∠CBG，根据同圆的半径相等得到OC=OB，于是得到∠OCB=∠OBC，等量代换得到∠OCB=∠CBG，根据平行线的判定得到OC//BG，即可得到结论；（2）由OC//BD，得到△OCF∽△BDF，△EOC∽△EBD，得到 ， ，根据直角三角形的性质即可得到结论；（3）如图2，过A作AH⊥DE于H，解直角三角形得到BD=3，DE=3 ，BE=6，在Rt△DAH中，AD= = = ．