题目内容
在矩形纸片ABCD中,AB=3 ,BC=6,沿EF折叠后,点C落在AB边上的点P处,点D落在点Q处,AD与PQ相交于点H,∠BPE=30°.
,BC=6,沿EF折叠后,点C落在AB边上的点P处,点D落在点Q处,AD与PQ相交于点H,∠BPE=30°.(1)BE的长为______,QF的长为______;
(2)四边形PEFH的面积为______

【答案】分析:(1)由于在Rt△PBE中,∠BPE=30°,设BE=x,然后根据三角函数的定义用x分别表示PE,PB,而BE+EC=BC,由此可以得到关于x的方程,解方程即可求出BE,接着求出PB,PA,PH,最后根据已知利用三角函数即可QF的值;
(2)根据已知可以得到四边形PEFH的面积等于梯形EFCD的面积减去三角形HFQ的面积,所以分别求出梯形EFCD的面积和三角形HFQ的面积即可.
解答:解:(1)设BE=x,在Rt△PBE中,∠BPE=30°,
∴PE=2x,PB= x,
x,
由题意得EC=EP=2x,
∵BE+EC=BC,
∴3x=6,x=2,即BE=2,
∴EC=4,PB=2
∴PA= ,
,
在Rt△APH中,∠APH=60°,
∴AH=3,PH=2
∴HQ=PQ-PH= ,
,
在Rt△HQF中,∠QHF=30°,
tan∠QHF= ,
,
∴QF=1;
(2)∵S梯形FECD= (1+4)×3
(1+4)×3 =
= ,
,
∴S△HFQ= ,
,
∴S四边形PEFH=S梯形FECD-S△HFQ= .
.
点评:此题考查综合解直角三角形,矩形的性质及翻折变换等知识点的掌握情况.
(2)根据已知可以得到四边形PEFH的面积等于梯形EFCD的面积减去三角形HFQ的面积,所以分别求出梯形EFCD的面积和三角形HFQ的面积即可.
解答:解:(1)设BE=x,在Rt△PBE中,∠BPE=30°,
∴PE=2x,PB=
 x,
x,由题意得EC=EP=2x,
∵BE+EC=BC,
∴3x=6,x=2,即BE=2,
∴EC=4,PB=2

∴PA=
 ,
,在Rt△APH中,∠APH=60°,
∴AH=3,PH=2

∴HQ=PQ-PH=
 ,
,在Rt△HQF中,∠QHF=30°,
tan∠QHF=
 ,
,∴QF=1;
(2)∵S梯形FECD=
 (1+4)×3
(1+4)×3 =
= ,
,∴S△HFQ=
 ,
,∴S四边形PEFH=S梯形FECD-S△HFQ=
 .
.点评:此题考查综合解直角三角形,矩形的性质及翻折变换等知识点的掌握情况.

练习册系列答案
相关题目
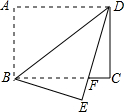 在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F,求BF的长.
在矩形纸片ABCD中,AB=6,BC=8.将矩形纸片沿BD折叠,使点A落在点E处,设DE与BC相交于点F,求BF的长.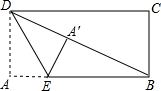 (2013•太原)如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为
(2013•太原)如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为 (2013•黄石模拟)如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F;
(2013•黄石模拟)如图,在矩形纸片ABCD中,AB=3,BC=4.把△BCD沿对角线BD折叠,使点C落在E处,BE交AD于点F; 如图,在矩形纸片ABCD中,AB=6,BC=8,现将其沿EF对折,使得点C与点A重合,则AF的长为
如图,在矩形纸片ABCD中,AB=6,BC=8,现将其沿EF对折,使得点C与点A重合,则AF的长为 动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.
动手操作:如图,在矩形纸片ABCD中,AB=3,AD=5.如图所示折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动.