题目内容
【题目】如图,在数轴上每相邻两点间的距离为一个单位长度,点![]() 、
、![]() 、
、![]() 、
、![]() 对应的数分别是
对应的数分别是![]() ,且
,且![]() .
.
(1)那么![]() ,
,![]() :
:
(2)点![]() 以
以![]() 个单位/秒的速度沿着数轴的正方向运动,
个单位/秒的速度沿着数轴的正方向运动,![]() 秒后点
秒后点![]() 以
以![]() 个单位/秒的速度也沿着数轴的正方向运动,当点
个单位/秒的速度也沿着数轴的正方向运动,当点![]() 到达点
到达点![]() 处立刻返回,与点
处立刻返回,与点![]() 在数轴的某点处相遇,求这个点对应的数;
在数轴的某点处相遇,求这个点对应的数;
(3)如果![]() 、
、![]() 两点以(2)中的速度同时向数轴的负方向运动,点
两点以(2)中的速度同时向数轴的负方向运动,点![]() 从图上的位置出发也向数轴的负方向运动,且始终保持
从图上的位置出发也向数轴的负方向运动,且始终保持![]() ,当点
,当点![]() 运动到
运动到![]() 时,点
时,点![]() 对应的数是多少?
对应的数是多少?

【答案】(1)![]() ,
,![]() ;(2)这个点对应的数为
;(2)这个点对应的数为![]() ;(3)点
;(3)点![]() 对应的数为
对应的数为![]()
【解析】
(1)根据数轴可知![]() ,然后代入等式求出a的值,再根据数轴确定出原点即可;
,然后代入等式求出a的值,再根据数轴确定出原点即可;
(2)根据相遇问题求得相遇时间,再计算即可求解;
(3)根据![]() 列出方程,再分两种情况讨论即可求解.
列出方程,再分两种情况讨论即可求解.
解:(1)由图可知:![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
则![]() ;
;
(2)由(1)可知:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
点![]() 运动到点
运动到点![]() 所花的时间为
所花的时间为![]() ,
,
设运动的时间为![]() 秒,
秒,
则![]() 对应的数为
对应的数为![]() ,
,
![]() 对应的数为:
对应的数为:![]() .
.
当![]() 、
、![]() 两点相遇时,
两点相遇时,![]() ,
,![]() ,
,
∴![]() .
.
答:这个点对应的数为![]() ;
;
(3)设运动的时间为![]()
![]() 对应的数为:
对应的数为:![]()
![]() 对应的数为:
对应的数为:![]()
∴![]()
∵![]()
∴![]()
∵![]() 对应的数为
对应的数为![]()
∴![]()
①当![]() ,
,![]() ;
;
②当![]() ,
,![]() ,不符合实际情况,
,不符合实际情况,
∴![]()
∴![]()
答:点![]() 对应的数为
对应的数为![]()

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
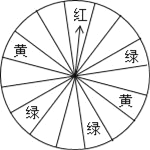
【题目】“六一”儿童节期间,某商厦为了吸引顾客,设立了一个可以自由转动的转盘(转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准哪个区域,顾客就可以获得相应的奖品.
颜色 | 奖品 |
红色 | 玩具熊 |
黄色 | 童话书 |
绿色 | 彩笔 |
小明和妈妈购买了125元的商品,请你分析计算:
(1)小明获得奖品的概率是多少?
(2)小明获得童话书的概率是多少?