题目内容
如图，在⊙O中，弦AB和CD相交于点P，若AP=4，PB=6，CP=3，则PD的长为分析：根据相交弦定理“圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等”进行计算．
解答：解：由相交弦定理得：PA•PB=PC•PD，∴DP=
=
=8．
| PA•PB |
| PC |
| 4×6 |
| 3 |
点评：本题主要考查相交弦定理：圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
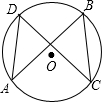已知：如图，在⊙O中，弦AD=BC．求证：AB=CD．
4、如图，在⊙O中，弦BC∥半径OA，AC与OB相交于M，∠C=20°，则∠AMB的度数为（ ）
标系．
如图，在⊙O中，弦AB=BC=CD，且∠ABC=140°，则∠AED=（ ）
如图，在⊙O中，弦AB与CD相交于点P，连接AC、DB．