题目内容
在周长相等的正三角形,正方形,圆中,面积最大的是________.
圆
分析:周长一定,设为l,根据周长分别求边长(半径),再计算图形的面积,比较大小.
解答:设周长为l,则:
周长为l的正三角形面积是 ×
× l×
l× l=
l= l2≈0.048l2;
l2≈0.048l2;
周长为l的正方形面积是( l)2=
l)2= l2≈0.0625l2;
l2≈0.0625l2;
周长为l的圆的面积是π×( )2=
)2=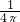 l2≈0.0796l2;
l2≈0.0796l2;
比较可知,面积最大的是圆.
点评:本题从数量上认证了,周长一定,圆的面积最大.
分析:周长一定,设为l,根据周长分别求边长(半径),再计算图形的面积,比较大小.
解答:设周长为l,则:
周长为l的正三角形面积是
 ×
× l×
l× l=
l= l2≈0.048l2;
l2≈0.048l2;周长为l的正方形面积是(
 l)2=
l)2= l2≈0.0625l2;
l2≈0.0625l2;周长为l的圆的面积是π×(
 )2=
)2=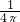 l2≈0.0796l2;
l2≈0.0796l2;比较可知,面积最大的是圆.
点评:本题从数量上认证了,周长一定,圆的面积最大.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目