题目内容
 如图,△ABC是直角边长为4的等腰直角三角形,直角边AB是半圆O1的直径,半圆O2过C点且与半圆O1相切,则图中阴影部分的面积是( )
如图,△ABC是直角边长为4的等腰直角三角形,直角边AB是半圆O1的直径,半圆O2过C点且与半圆O1相切,则图中阴影部分的面积是( )分析:连接O1E,O2D,O1O2.则阴影部分的面积=(直角三角形ABC的面积-扇形O2PD的面积-三角形O2CD的面积-扇形O1AE的面积-三角形O1BE的面积)+(扇形O2CD的面积-三角形O2CD的面积+扇形O1BE的面积-三角形O1BE的面积).根据等腰直角三角形的性质和同圆的半径相等,知三角形O2CD和三角形O1BE都是等腰直角三角形.设半圆O2的半径是x,根据勾股定理列方程即可求解.
解答:解:连接O1E,O2D,O1O2.
设半圆O2的半径是x,根据勾股定理,得22+(2-x)2=(2+x)2,
解得:x=
.
∵△ABC是等腰直角三角形,
∴∠B=∠C=45°.
∴∠O2DC=∠C=45°,∠O1EB=∠B=45°.
∴∠CO2D=∠EO1B=90°.
∴阴影部分的面积=直角三角形ABC的面积-2(直角三角形CO2D的面积+直角三角形BO1E的面积)
=
×42-2(
×
-
×4)=
.
故选C.
设半圆O2的半径是x,根据勾股定理,得22+(2-x)2=(2+x)2,
解得:x=
| 4 |
| 3 |
∵△ABC是等腰直角三角形,
∴∠B=∠C=45°.
∴∠O2DC=∠C=45°,∠O1EB=∠B=45°.
∴∠CO2D=∠EO1B=90°.
∴阴影部分的面积=直角三角形ABC的面积-2(直角三角形CO2D的面积+直角三角形BO1E的面积)
=
| 1 |
| 2 |
| 1 |
| 2 |
| 16 |
| 9 |
| 1 |
| 2 |
| 28 |
| 9 |
故选C.
点评:此题关键是能够根据勾股定理求得半圆O2的半径,同时能够发现△O2CD和△O1BE都是直角三角形.

练习册系列答案
相关题目

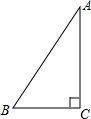 .
. 如图,△ABC是直角三角形,∠BAC=90°,AD、AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm.
如图,△ABC是直角三角形,∠BAC=90°,AD、AE分别是△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm.