题目内容
说理填空题:如图,EC=EB,∠CDA=120°,DF∥BE,且DF平分∠CDA,试说明AD与BC平行的理由.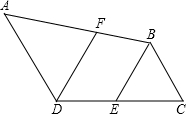 解:∵DF平分∠CDA,∠CDA=120°(已知)
解:∵DF平分∠CDA,∠CDA=120°(已知)∴∠FDC=
| 1 | 2 |
∵DF∥BE,(已知),
∴∠FDC=∠
又∵EC=EB,(已知)
∴△BCE为等边三角形.
∴∠C=°
∵∠CDA=120°(已知)
∴∠C+∠CDA=180°
∴AD∥BC
分析:根据角平分线的性质、平行线的性质、等边三角形的判定、平行线的判定依次推理论证即可得出结论.
解答:解:∵DF平分∠CDA,∠CDA=120°(已知)
∴∠FDC=
∠CDA=60°(角平分线定义 ),
∵DF∥BE,(已知)
∴∠FDC=∠BEC=60°(两直线平行,同位角相等).
又∵EC=EB,(已知)
∴△BCE为等边三角形(有一个角为60°的等腰三角形是等边三角形),
∴∠C=60° ( 等边三角形的每一个内角都等于 60° ),
∵∠CDA=120°(已知)
∴∠C+∠CDA=180°,
∴AD∥BC(同旁内角互补,两直线平行).
∴∠FDC=
| 1 |
| 2 |
∵DF∥BE,(已知)
∴∠FDC=∠BEC=60°(两直线平行,同位角相等).
又∵EC=EB,(已知)
∴△BCE为等边三角形(有一个角为60°的等腰三角形是等边三角形),
∴∠C=60° ( 等边三角形的每一个内角都等于 60° ),
∵∠CDA=120°(已知)
∴∠C+∠CDA=180°,
∴AD∥BC(同旁内角互补,两直线平行).
点评:本题主要考查了角平分线的性质、平行线的性质、等边三角形的判定、平行线的判定,比较综合,难度适中.

练习册系列答案
相关题目
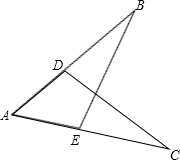 说理题:
说理题: 解:∵DF平分∠CDA,∠CDA=120°(已知)
解:∵DF平分∠CDA,∠CDA=120°(已知) ∠=________,
∠=________,

