题目内容
阅读材料：
如果x1，x2是一元二次方程ax2+bx+c=0的两根，那么有
．
这是一元二次方程根与系数的关系，我们利用它可以用来解题．
已知x1，x2是方程x2-4x+2=0的两根，求：（1）
的值；（2）（x1-x2）2的值．
解：∵x1+x2=4，x1x2=2．
（1）
；
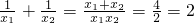（2）（x1-x2）2=（x1+x2）2-4x1x2=42-4×2=8．
分析：根据一元二次方程ax2+bx+c=0的根与系数关系即韦达定理可得x1+x2
=4，x1x2=
=2，把代数式变形成与两根之和和两根之积有关的式子，代入两根之和与两根之积，求得代数式的值．
点评：本题主要考查一元二次方程ax2+bx+c=0的根与系数关系即韦达定理，两根之和是，两根之积是 ，难度适中．
（1）
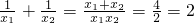；（2）（x1-x2）2=（x1+x2）2-4x1x2=42-4×2=8．
分析：根据一元二次方程ax2+bx+c=0的根与系数关系即韦达定理可得x1+x2
=4，x1x2==2，把代数式变形成与两根之和和两根之积有关的式子，代入两根之和与两根之积，求得代数式的值．点评：本题主要考查一元二次方程ax2+bx+c=0的根与系数关系即韦达定理，两根之和是
，两根之积是 ，难度适中． 
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目