题目内容
 (2009•西藏)如图,在高楼前D点测得楼顶的仰角为30°,向高楼前进60米到C点,又测得仰角为45°,则该高楼的高度为( )米.
(2009•西藏)如图,在高楼前D点测得楼顶的仰角为30°,向高楼前进60米到C点,又测得仰角为45°,则该高楼的高度为( )米.分析:由于AB是Rt△ABD和Rt△ABC的公共直角边,可在Rt△ABC中,根据∠ACB的正切值,用AB表示出BC的长;同理可在Rt△ABD中,根据∠D的度数,用AB表示出BD的长;根据CD=BD-BC,即可求得AB的长.
解答:解:Rt△ABC中,∠ACB=45°,
∴BC=AB;
Rt△ABD中,∠ADB=30°,
∴BD=AB÷tan30°=
AB,
∴DC=BD-BC=(
-1)AB=60米.
∴AB=
=30(
+1)米,
故选C.
∴BC=AB;
Rt△ABD中,∠ADB=30°,
∴BD=AB÷tan30°=
| 3 |
∴DC=BD-BC=(
| 3 |
∴AB=
| 60 | ||
|
| 3 |
故选C.
点评:此题主要考查了仰角的定义及其解直角三角形的应用,解题时首先正确理解仰角的定义,然后利用三角函数和已知条件构造方程解决问题.当两个直角三角形有公共边时,利用这条公共边进行求解是解此类题的常用方法.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 (2009•西藏)如图,已知a∥b,∠1=50°,那么∠2的度数是( )
(2009•西藏)如图,已知a∥b,∠1=50°,那么∠2的度数是( )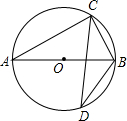 (2009•西藏)如图,AB是圆O的直径,点C、D在圆O上,∠ABC=65°,则∠D的度数是( )
(2009•西藏)如图,AB是圆O的直径,点C、D在圆O上,∠ABC=65°,则∠D的度数是( ) (2009•西藏)如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为( )
(2009•西藏)如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为( ) (2009•西藏)如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,DB=2,则DE:BC的值为
(2009•西藏)如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,DB=2,则DE:BC的值为 (2009•西藏)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
(2009•西藏)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.