题目内容
李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.
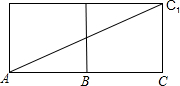
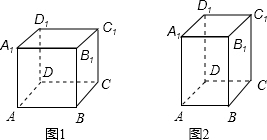
(1)如图1,正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处;
(2)如图2,圆锥的母线长为4cm,底面半径r= cm,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.
cm,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.
(3)如图3,是一个没有上盖的圆柱形食品盒,一只蚂蚁在盒外表面的A处,它想吃到盒内表面对侧中点B处的食物,已知盒高10cm,底面圆周长为32cm,A距下底面3cm.

解:(1)
(2)解:由已知条件:圆锥的母线长为4cm,底面半径r= cm,
cm,
∴2×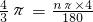 ,
,
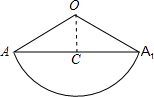
∴可求出圆锥侧面展开图中圆心角:n=∠AOA1=120°,
∴∠AOC=60°,sin60°= =
= ,
,
∴进一步可求得最短的路程为AA1= .
.
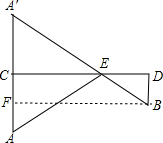
(3)如图,作出点A关于CD的对称点A'.
根据题意求出BF=CD=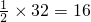 ,
,
可构造直角三角形或利用相似三角形等有关知识
求出BA'=20cm,
所以蚂蚁吃到食物的爬行的最短路程为AE+BE=BA'=20cm
分析:(1)根据正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处,即展开正方体,蚂蚁爬△ACC1的对角线,求出即可.
(2)首先根据圆锥的底面周长等于展开图的弧长,可求出圆锥侧面展开图中圆心角:n=∠AOA1=120°,进而得出AA1的长;
(3)作出点A关于CD的对称点A',可构造直角三角形或利用相似三角形等有关知识,进而得出求出BA'=20cm,即是所求.
点评:此题主要考查了平面展开图中最短路径问题,这是中考中热点问题,找出展开图的与原图形对应情况是解决问题的关键.


(2)解:由已知条件:圆锥的母线长为4cm,底面半径r=
 cm,
cm,∴2×
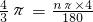 ,
,∴可求出圆锥侧面展开图中圆心角:n=∠AOA1=120°,
∴∠AOC=60°,sin60°=
 =
= ,
,∴进一步可求得最短的路程为AA1=
 .
.
(3)如图,作出点A关于CD的对称点A'.
根据题意求出BF=CD=
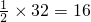 ,
,可构造直角三角形或利用相似三角形等有关知识
求出BA'=20cm,
所以蚂蚁吃到食物的爬行的最短路程为AE+BE=BA'=20cm

分析:(1)根据正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处,即展开正方体,蚂蚁爬△ACC1的对角线,求出即可.
(2)首先根据圆锥的底面周长等于展开图的弧长,可求出圆锥侧面展开图中圆心角:n=∠AOA1=120°,进而得出AA1的长;
(3)作出点A关于CD的对称点A',可构造直角三角形或利用相似三角形等有关知识,进而得出求出BA'=20cm,即是所求.
点评:此题主要考查了平面展开图中最短路径问题,这是中考中热点问题,找出展开图的与原图形对应情况是解决问题的关键.

练习册系列答案
相关题目


 cm,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A;
cm,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A;
 cm,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A;
cm,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A;