题目内容
在函数y=
（k＞0）的图象上有三点A1（x1，y1 ）、A2（x2，y2）、A3（x3，y3 ），已知x1＜x2＜0＜x3，则y1、y2、y3之间的关系为
| k | x |
y2＜y1＜y3
y2＜y1＜y3
（用＜号连接）分析：根据题意画出图形，再根据函数的增减性解答即可．
解答：
解：∵k＞0，函数图象如图，
∴图象在第一、三象限，在每个象限内，y随x的增大而减小，
∵x1＜x2＜0＜x3，
∴y2＜y1＜y3．
故答案为：y2＜y1＜y3．
解：∵k＞0，函数图象如图，∴图象在第一、三象限，在每个象限内，y随x的增大而减小，
∵x1＜x2＜0＜x3，
∴y2＜y1＜y3．
故答案为：y2＜y1＜y3．
点评：本题考查了由反比例函数的性质确定函数图象上点的坐标特征，综合性较强．
练习册系列答案
相关题目
如图，已知正方形OABC的面积为9，点O为坐标原点，点A在x轴上，点C在y轴上，点B在函数
如图，A、B两点在函数已知点（2，-6）在函数y=kx的图象上，则函数y=
的图象在（ ）
| k |
| x |
| A、第一、三象限 |
| B、第二、三象限 |
| C、第二、四象限 |
| D、第一、四象限 |
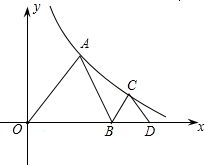如图，△AOB和△BCD都是等边三角形，点A、C在函数