题目内容
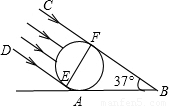
23、在生活中需测量一些球的足球、篮球）的直径．某校研究性学习小组，通过实验发现下面的测量方法：如图，将球放在水平的桌面上，在阳光的斜射下，得到球的影子AB，设光线DA、CB分别与球相切于点E、F，则EF即为球的直径．若测得AB的长为41、5cm，∠ABC=37°．请你计算出球的直径（精确到1cm）．分析：利用37°的正弦值可近似的求出球的直径EF．
解答：解：如图，过A作AM⊥BF于M，
∵光线DA、CB分别与球相切于点E、F，并且AD∥CB，
∴EF=AM，
在Rt△BAM中，
EF=AM=AB•sin37°≈25cm．
答：球的直径约为25cm
∵光线DA、CB分别与球相切于点E、F，并且AD∥CB，
∴EF=AM，
在Rt△BAM中，
EF=AM=AB•sin37°≈25cm．
答：球的直径约为25cm
点评：用到的知识点为：圆的切线垂直于经过切点的半径；一个角的正弦值等于这个角的对边与斜边之比．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
的直径．若测得AB的长为41.5cm，∠ABC=37°．请你计算出球的直径（精确到1cm）；
的直径．若测得AB的长为41.5cm，∠ABC=37°．请你计算出球的直径（精确到1cm）；
