ΧβΡΩΡΎ»ί
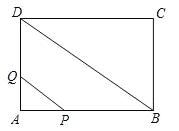
ΓΨΧβΡΩΓΩ»γΆΦ,≈ΉΈοœΏ![]() ΒΡΕ‘≥Τ÷αΈΣ÷±œΏx=2,«“≈ΉΈοœΏΨ≠ΙΐA(1,0),C(0,5)ΝΫΒψΘ§”κx÷αΫΜ”ΎΒψB.
ΒΡΕ‘≥Τ÷αΈΣ÷±œΏx=2,«“≈ΉΈοœΏΨ≠ΙΐA(1,0),C(0,5)ΝΫΒψΘ§”κx÷αΫΜ”ΎΒψB.
(1)»τ÷±œΏy=mx+nΨ≠ΙΐB. CΝΫΒψΘ§«σ÷±œΏBCΚΆ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
(2)…ηΒψPΈΣ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§Ν§Ϋ”PBΓΔPCΘ§»τΓςBPC «“‘BCΈΣ÷±Ϋ«±ΏΒΡ÷±Ϋ«»ΐΫ«–ΈΘ§«σ¥Υ ±ΒψPΒΡΉχ±ξΘΜ
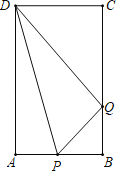
(3)‘Ύ≈ΉΈοœΏ…œBCΕΈ”–Νμ“ΜΗωΕ·ΒψQΘ§“‘ΒψQΈΣ‘≤–ΡΉςQΘ§ ΙΒΟQ”κ÷±œΏBCœύ«–Θ§‘Ύ‘ΥΕ·ΒΡΙΐ≥Χ÷– «Ζώ¥φ‘Ύ“ΜΗωΉν¥σQ?»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΉν¥σQΒΡΑκΨΕΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
ΓΨ¥πΑΗΓΩ(1) ![]() (2) PΒΡΉχ±ξΈΣ(3,8)Μρ(-2,7)ΘΜ (3)
(2) PΒΡΉχ±ξΈΣ(3,8)Μρ(-2,7)ΘΜ (3)![]()
ΓΨΫβΈωΓΩ
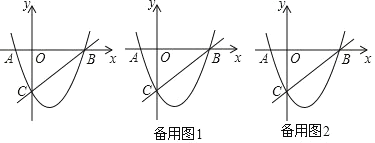
Θ®1Θ©ΗυΨίΕ‘≥Τ÷αΦΑAΒψΉχ±ξΒΟ≥ωBΒψΉχ±ξΘ§¥”ΕχΒΟ≥ω÷±œΏBCΫβΈω ΫΘ§‘Ό”…AΓΔBΓΔC»ΐΒψΉχ±ξΒΟ≥ω≈ΉΈοœΏΫβΈω ΫΘΜ
Θ®2Θ©Ζ÷±πΙΐBΓΔCΝΫΒψΉςBCΒΡ¥ΙœΏΘ§ΒΟ≥ω¥ΙœΏΒΡΫβΈω ΫΘ§”κ≈ΉΈοœΏΫβΈω ΫΝΣΝΔΫβ≥ωPΒψΘΜ
Θ®3Θ©ΤΫ“ΤBCΒΫ”κ≈ΉΈοœΏΗ’ΚΟœύ«–÷°¥ΠΘ§¥Υ ±ΒΡ«–ΒψΦ¥ΈΣQΒψΘ§¥Υ ±QΒψΨύBCΒΡΨύάκΉν¥σΘ§“≤ΨΆ «ΑκΨΕΉν¥σΘ°‘Υ”ΟΒ»ΟφΜΐΖ®Ϋχ––¥ΠάμΘ°…η«–œΏ”κy÷αΒΡΫΜΒψΈΣHΘ§‘ρΓςHBC”κΓςQBCΒΡΟφΜΐœύΒ»Θ§Υψ≥ωΟφΜΐΘ§‘Ό“‘BCΈΣΒΉΘ§Υψ≥ωBC±Ώ…œΒΡΗΏΦ¥ΈΣ¥πΑΗΘ°
(1)ΓΏΕ‘≥Τ÷αΈΣx=2,«“≈ΉΈοœΏΨ≠ΙΐA(1,0)Θ§
ΓύB(5,0).
Α―B(5,0),C(0,5)Ζ÷±π¥ζ»κy=mx+nΒΟ![]() ,ΫβΒΟΘΚ
,ΫβΒΟΘΚ![]() Θ§
Θ§
Γύ÷±œΏBCΒΡΫβΈω ΫΈΣy=x5.
…ηy=a(x5)(x+1)Θ§Α―ΒψCΒΡΉχ±ξ¥ζ»κΒΟΘΚ5a=5Θ§ΫβΒΟΘΚa=1Θ§
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚ![]() .
.
Θ®2Θ©ΔΌΙΐΒψCΉς![]() ,ΫΜ≈ΉΈοœΏ”ΎΒψ
,ΫΜ≈ΉΈοœΏ”ΎΒψ![]() Θ§»γΆΦΘ§
Θ§»γΆΦΘ§

‘ρ÷±œΏ![]() ΒΡΫβΈω ΫΈΣy=x5,
ΒΡΫβΈω ΫΈΣy=x5,
”…![]() ,ΫβΒΟΘΚ
,ΫβΒΟΘΚ (…α»Ξ),
(…α»Ξ),  Θ§
Θ§
Γύ![]() (3,8)ΘΜ
(3,8)ΘΜ
ΔΎΙΐΒψBΉς![]() ,ΫΜ≈ΉΈοœΏ”Ύ
,ΫΜ≈ΉΈοœΏ”Ύ![]() Θ§»γΆΦΘ§
Θ§»γΆΦΘ§

‘ρ![]() ΒΡΫβΈω ΫΈΣy=x+5Θ§
ΒΡΫβΈω ΫΈΣy=x+5Θ§
”…![]() ,ΫβΒΟΘΚ
,ΫβΒΟΘΚ (…α»Ξ),
(…α»Ξ),  Θ§
Θ§
Γύ![]() (-2,7)ΘΜ
(-2,7)ΘΜ
ΓύPΒΡΉχ±ξΈΣ(3,8)Μρ(-2,7)ΘΜ
Θ®3Θ©”…Χβ“βΩ…÷Σ,QΒψΨύάκBCΉν‘Ε ±,ΑκΨΕΉν¥σ.ΤΫ“Τ÷±œΏBC, ΙΤδ”κ≈ΉΈοœΏ÷Μ”–“ΜΗωΙΪΙ≤ΒψQ(Φ¥œύ«–)Θ§…ηΤΫ“ΤΚσΒΡ÷±œΏΫβΈω ΫΈΣy=x+tΘ§
”…![]() ,œϊ»Ξy’ϊάμΒΟ
,œϊ»Ξy’ϊάμΒΟ![]() Θ§
Θ§
Γς=![]() ,ΫβΒΟ
,ΫβΒΟ![]() Θ§
Θ§
ΓύΤΫ“ΤΚσ”κ≈ΉΈοœΏœύ«– ±ΒΡ÷±œΏΫβΈω ΫΈΣ![]() ,«“Q
,«“Q![]() Θ§
Θ§
Ν§Ϋ”QCΓΔQBΘ§ΉςQEΓΆBC”ΎEΘ§»γΆΦΘ§

…η÷±œΏ![]() ”κy÷αΒΡΫΜΒψΈΣHΘ§Ν§Ϋ”HBΘ§
”κy÷αΒΡΫΜΒψΈΣHΘ§Ν§Ϋ”HBΘ§
‘ρSΓςHBC=![]() BOCHΘ§
BOCHȧ
ΓΏCH=5(![]() )=
)=![]() Θ§
Θ§
ΓύSΓςHBC=![]() ΓΝ5ΓΝ
ΓΝ5ΓΝ![]() =
=![]() Θ§
Θ§
ΓύSΓςQBC=SΓςHBC=![]() Θ§
Θ§
ΓΏSΓςQBC=![]() BCQE, BC=
BCQE, BC=![]() Θ§
Θ§
ΓύQE=![]() Θ§
Θ§
Φ¥Ήν¥σΑκΨΕΈΣ![]() .
.

 –Γ―ß―ßœΑΚΟΑο ÷œΒΝ–¥πΑΗ
–Γ―ß―ßœΑΚΟΑο ÷œΒΝ–¥πΑΗ –Γ―ßΆ§≤Ϋ»ΐΝΖΚΥ–ΡΟήΨμœΒΝ–¥πΑΗ
–Γ―ßΆ§≤Ϋ»ΐΝΖΚΥ–ΡΟήΨμœΒΝ–¥πΑΗ