题目内容
 如图,点G是等边△ABC的重心,过点G作BC的平行线,分别交AB、AC与点D、E,在BC边上确定一点M,使△BDM∽△CEM(但不全等),则S△BDM:S△CEM=________.
如图,点G是等边△ABC的重心,过点G作BC的平行线,分别交AB、AC与点D、E,在BC边上确定一点M,使△BDM∽△CEM(但不全等),则S△BDM:S△CEM=________.
(7+3  ):2或(7-3
):2或(7-3  ):2
):2
分析:首先由点G是等边△ABC的重心,DE∥BC,根据平行线分线段成比例定理与三角形重心的性质,即可得AB=BC=AC,∠B=∠C=60°, ,然后由相似三角形的对应边成比例,即可求得答案.
,然后由相似三角形的对应边成比例,即可求得答案.
解答: 解:∵点G是等边△ABC的重心,DE∥BC,
解:∵点G是等边△ABC的重心,DE∥BC,
∴AB=BC=AC,∠B=∠C=60°, ,
,
∴BD= BC,EC=
BC,EC= BC,
BC,
当△BDM∽△CME时,则 ,
,
设BD=a,CM=x,则CE=a,BC=3a,BM=3a-x,
∴ ,
,
解得:x= a,
a,
∴当BM= a时,CM=
a时,CM= a,则S△BDM:S△CEM=BM:CM=
a,则S△BDM:S△CEM=BM:CM=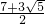 ;
;
当BM= a时,CM=
a时,CM= a,则S△BDM:S△CEM=
a,则S△BDM:S△CEM= .
.
故答案为:(7+3 ):2或(7-3
):2或(7-3  ):2.
):2.
点评:此题考查了等边三角形的性质,三角形重心的性质,平行线分线段成比例定理以及相似三角形的性质等知识.此题综合性很强,难度适中,解题的关键是注意数形结合思想与方程思想的应用.
 ):2或(7-3
):2或(7-3  ):2
):2分析:首先由点G是等边△ABC的重心,DE∥BC,根据平行线分线段成比例定理与三角形重心的性质,即可得AB=BC=AC,∠B=∠C=60°,
 ,然后由相似三角形的对应边成比例,即可求得答案.
,然后由相似三角形的对应边成比例,即可求得答案.解答:
 解:∵点G是等边△ABC的重心,DE∥BC,
解:∵点G是等边△ABC的重心,DE∥BC,∴AB=BC=AC,∠B=∠C=60°,
 ,
,∴BD=
 BC,EC=
BC,EC= BC,
BC,当△BDM∽△CME时,则
 ,
,设BD=a,CM=x,则CE=a,BC=3a,BM=3a-x,
∴
 ,
,解得:x=
 a,
a,∴当BM=
 a时,CM=
a时,CM= a,则S△BDM:S△CEM=BM:CM=
a,则S△BDM:S△CEM=BM:CM=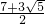 ;
;当BM=
 a时,CM=
a时,CM= a,则S△BDM:S△CEM=
a,则S△BDM:S△CEM= .
.故答案为:(7+3
 ):2或(7-3
):2或(7-3  ):2.
):2.点评:此题考查了等边三角形的性质,三角形重心的性质,平行线分线段成比例定理以及相似三角形的性质等知识.此题综合性很强,难度适中,解题的关键是注意数形结合思想与方程思想的应用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 21、如图,点D是等边三角形ABC内的一点,将△BDC绕点C顺时针旋转60°,试画出旋转后的三角形,并指出图中的全等图形以及它们的对应顶点、对应边和对应角.
21、如图,点D是等边三角形ABC内的一点,将△BDC绕点C顺时针旋转60°,试画出旋转后的三角形,并指出图中的全等图形以及它们的对应顶点、对应边和对应角. 16、如图,点P是等边三角形ABC内一点,BP=5cm,△PAB绕点B旋转后能与△MCB重合,连接PM,则PM=
16、如图,点P是等边三角形ABC内一点,BP=5cm,△PAB绕点B旋转后能与△MCB重合,连接PM,则PM= 21、如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.以OC为一边作等边三角形OCD,连接AC、AD.
21、如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.以OC为一边作等边三角形OCD,连接AC、AD. (2011•清流县质检)星期天,小明在解答下列题目时卡壳了.
(2011•清流县质检)星期天,小明在解答下列题目时卡壳了. 得到线段CD,连接OD、AD.
得到线段CD,连接OD、AD.