题目内容
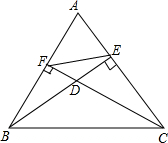 己知BE、CF分别是△ABC的边AC、AB上的高,高BE、CF所在的直线相交于点D(如图)
己知BE、CF分别是△ABC的边AC、AB上的高,高BE、CF所在的直线相交于点D(如图)
(1)当∠BAC是锐角时,求证:△ABC∽△AEF;
(2)当∠BAC是钝角时,(1)中的结论还成立吗?直接写出结论,无需说明理由;
(3)如果∠BAC=60°,求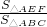 的值.
的值.
 解:(1)∵AB⊥CF,BE⊥AC,
解:(1)∵AB⊥CF,BE⊥AC,∴∠AEB=∠AFC=90°,
∵∠A=∠A,
∴△ABE∽△ACF,
∴
 =
= ,
,∴
 =
= ,
,∴△ABC∽△AEF;
(2)△ABC∽△AEF成立,
如图:

(3)在Rt△ABE中,
∵∠BAC=60°,
∴∠ABE=30°,
∴
 =
= ,
,∴
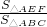 =
= .
.分析:(1)根据BE、CF分别是△ABC的边AC、AB上的高,得出∠AEB=∠AFC=90°,即可求出△ABE∽△ACF,得出
 =
= ,从而证出△ABC∽△AEF;
,从而证出△ABC∽△AEF;(2)先作出图形,证明的方法和(1)一样.
(3)在Rt△ABE中,根据∠BAC=60°,得出∠ABE=30°,从而得出
 =
= ,即可求出
,即可求出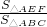 的值.
的值.点评:本题考查了相似三角形的判定与性质:有两条边对应成比例并且夹角相等的两个三角形相似;相似三角形的对应边成比例,对应角相等.

练习册系列答案
相关题目
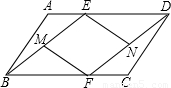
 己知:如图,E、F分别是?ABCD的AD、BC边上的点,且AE=CF.
己知:如图,E、F分别是?ABCD的AD、BC边上的点,且AE=CF.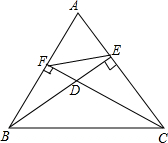 (2012•嘉定区一模)己知BE、CF分别是△ABC的边AC、AB上的高,高BE、CF所在的直线相交于点D(如图)
(2012•嘉定区一模)己知BE、CF分别是△ABC的边AC、AB上的高,高BE、CF所在的直线相交于点D(如图)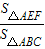 的值.
的值.